题目内容
 (1)在Rt△ABC中,∠ACB=90°,CD⊥AB于D,设AC=b,BC=a,AB=c,CD=h,
(1)在Rt△ABC中,∠ACB=90°,CD⊥AB于D,设AC=b,BC=a,AB=c,CD=h,求证:a+b<c+h.
(2)解方程:|x-2|+|x+1|=5.
考点:勾股定理,含绝对值符号的一元一次方程
专题:
分析:(1)根据三角形的面积公式求出ab=ch,利用勾股定理可得a2+b2=c2,再利用完全平方公式整理即可得证;
(2)分x<-1,-1<x<2,x>2三种情况,根据绝对值的性质去掉绝对值号,然后解一元一次方程即可.
(2)分x<-1,-1<x<2,x>2三种情况,根据绝对值的性质去掉绝对值号,然后解一元一次方程即可.
解答:(1)证明:∵CD⊥AB,∠ACB=90°,
∴S△ABC=
ab=
ch,
∴ab=ch,
∵∠ACB=90°,
∴a2+b2=c2,
∴(a+b)2=a2+2ab+b2=c2+2ch,
(c+h)2=c2+2ch+h2,
∵a、b、c、h都是正数,
∴(a+b)2<(c+h)2,
∴a+b<c+h;
(2)解:x<-1时,x+1<0,x-2<0,
原方程化为-(x-2)-(x+1)=5,
解得x=-2,
-1<x<2时,x+1>0,x-2<0,
原方程化为-(x-2)+(x+1)=5,
方程无解,
x>2时,x+1>0,x-2>0,
原方程化为(x-2)+(x+1)=5,
解得x=3,
所以,原方程的解是x=-2或x=3.
∴S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
∴ab=ch,
∵∠ACB=90°,
∴a2+b2=c2,
∴(a+b)2=a2+2ab+b2=c2+2ch,
(c+h)2=c2+2ch+h2,
∵a、b、c、h都是正数,
∴(a+b)2<(c+h)2,
∴a+b<c+h;
(2)解:x<-1时,x+1<0,x-2<0,
原方程化为-(x-2)-(x+1)=5,
解得x=-2,
-1<x<2时,x+1>0,x-2<0,
原方程化为-(x-2)+(x+1)=5,
方程无解,
x>2时,x+1>0,x-2>0,
原方程化为(x-2)+(x+1)=5,
解得x=3,
所以,原方程的解是x=-2或x=3.
点评:(1)考查了勾股定理,主要利用了三角形的面积,完全平方公式,以及勾股定理,配方整理出(a+b)2和(c+h)2是解题的关键;
(2)考查了含绝对值符号的方程,难点在于分段讨论并去掉绝对值号.
(2)考查了含绝对值符号的方程,难点在于分段讨论并去掉绝对值号.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
下列运算正确的是( )
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
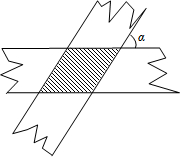 如图:两张宽度都为3cm的纸条交叉重叠在一起,其中∠α=60°,求重叠(阴影)部分的面积?(结果保留根号)
如图:两张宽度都为3cm的纸条交叉重叠在一起,其中∠α=60°,求重叠(阴影)部分的面积?(结果保留根号)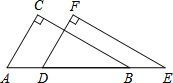 两个全等的直角三角形ABC和DEF重合在一起,其中∠ACB=∠DFE=90°,∠BAC=∠EDF=60°,AC=DF=1.如图,固定△ABC不动,将△DEF沿线段AB向右平移,直至D、B两点重合为止.在此过程中,当点D不与A、B两点重合时,可作四边形CDBF.
两个全等的直角三角形ABC和DEF重合在一起,其中∠ACB=∠DFE=90°,∠BAC=∠EDF=60°,AC=DF=1.如图,固定△ABC不动,将△DEF沿线段AB向右平移,直至D、B两点重合为止.在此过程中,当点D不与A、B两点重合时,可作四边形CDBF.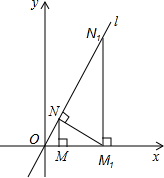 如图,已知直线l:
如图,已知直线l: