题目内容
 如图,长方形纸片ABCD中,AD=4cm,AB=10cm,按如图所示方式折叠,使点B与点D重合,折痕为EF,则三角形DEF的面积为
如图,长方形纸片ABCD中,AD=4cm,AB=10cm,按如图所示方式折叠,使点B与点D重合,折痕为EF,则三角形DEF的面积为考点:翻折变换(折叠问题)
专题:
分析:设AE=x,DE=10-x,则在直角△ADE中根据勾股定理列出关于x的关系式,求出x,即可求得BE的值,求出△BEF的面积即可得出△DEF的面积.
解答: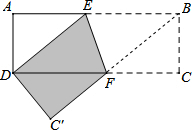 解:设AE=x,BE=DE=10-x,
解:设AE=x,BE=DE=10-x,
则在直角△ADE中,x2+42=(10-x)2
解得x=4.2cm,
即BE=DE=10cm-4.2cm=5.8cm,
即DE=5.8cm.
∵B沿EF折叠后和D重合,
∴△DEF与△BEF的面积相等,
∴S△DEF=S△BEF=
×BE×BC=
×5.8cm×4cm=11.6cm2.
故答案是:11.6.
 解:设AE=x,BE=DE=10-x,
解:设AE=x,BE=DE=10-x,则在直角△ADE中,x2+42=(10-x)2
解得x=4.2cm,
即BE=DE=10cm-4.2cm=5.8cm,
即DE=5.8cm.
∵B沿EF折叠后和D重合,
∴△DEF与△BEF的面积相等,
∴S△DEF=S△BEF=
| 1 |
| 2 |
| 1 |
| 2 |
故答案是:11.6.
点评:本题考查了长方形对角线相等且互相平分的性质,直角三角形面积的计算,勾股定理在直角三角形中的运用,本题中求AE的长是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
根据下列条件列出的代数式,错误的是( )
| A、a、b两数的平方差为a2-b2 |
| B、a与b两数差的平方为(a-b)2 |
| C、a与b的平方的差为a2-b2 |
| D、a与b的差的平方为(a-b)2 |
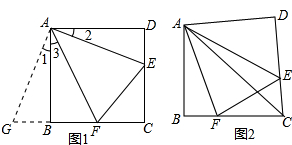
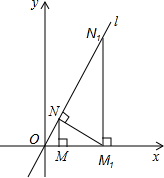 如图,已知直线l:
如图,已知直线l: