��Ŀ����
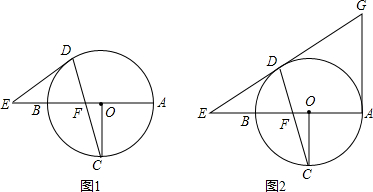
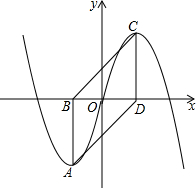
17��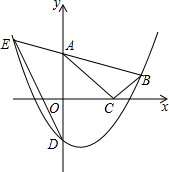 ��ͼ����ƽ��ֱ������ϵ�У�Rt��ABC�Ķ���A��C�ֱ���y�ᡢx���ϣ���ACB=90�㣬OA=$\sqrt{3}$��������y=ax2-ax-a������B��2��$\frac{\sqrt{3}}{3}$������y�ύ�ڵ�D��
��ͼ����ƽ��ֱ������ϵ�У�Rt��ABC�Ķ���A��C�ֱ���y�ᡢx���ϣ���ACB=90�㣬OA=$\sqrt{3}$��������y=ax2-ax-a������B��2��$\frac{\sqrt{3}}{3}$������y�ύ�ڵ�D����1���������ߵı���ʽ��
��2����B����ֱ��AC�ĶԳƵ��Ƿ����������ϣ���˵�����ɣ�
��3���ӳ�BA���������ڵ�E������ED����˵��ED��AC�����ɣ�
��4����P�ӵ�O��ʼ��OC�˶�������Cֹͣ������AP������B��BF��AP��F����ֱ��д����F���˶�·������
���� ��1���ѵ�B����������ʽ���a��ֵ���ɣ�
��2���������B����ֱ��AC�ĶԳƵ����꣬�ٴ��������߽����жϼ��ɣ�
��3�����������ߺ�ֱ��AB�����E���֤꣬����ADE=��CAO���ɣ�
��4���жϵ�F���˶��켣��������ݻ�����ʽ����������ɣ�
��� �⣺��1��������y=ax2-ax-a������B��2��$\frac{\sqrt{3}}{3}$����
��$\frac{\sqrt{3}}{3}$=4a-2a-a��
��a=$\frac{\sqrt{3}}{3}$��
�������ߵı���ʽΪ��y=$\frac{\sqrt{3}}{3}$x2-$\frac{\sqrt{3}}{3}$x-$\frac{\sqrt{3}}{3}$��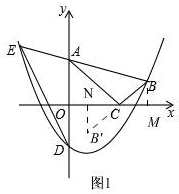
��2����ͼ1��
����B��x��Ĵ��ߣ�����ΪM��
��OC=m����CM=2-m��
�ɡ�ACB=90�㣬OA��OC��BM��CM����֤��AOC�ס�CMB��
��$\frac{OA}{OC}=\frac{CM}{BM}$��
��$\frac{\sqrt{3}}{m}=\frac{2-m}{\frac{\sqrt{3}}{3}}$��
��ã�m=1��
��C��1��0����
�������㷨����ֱ��AC��y=-$\sqrt{3}$x+$\sqrt{3}$��$\sqrt{3}$x+y-$\sqrt{3}$=0��
�ӳ�BC���� B�䣬ʹ��CB��=CB������B����x��Ĵ��ߣ�����ΪN��
����CN=CM=1��NB��=$\frac{\sqrt{3}}{3}$��
���B����ֱ��AC�ĶԳƵ�Ϊ����0��-$\frac{\sqrt{3}}{3}$����
y=$\frac{\sqrt{3}}{3}$x2-$\frac{\sqrt{3}}{3}$x-$\frac{\sqrt{3}}{3}$����x=0ʱ��y=-$\frac{\sqrt{3}}{3}$��
���B����ֱ��AC�ĶԳƵ����������ϣ�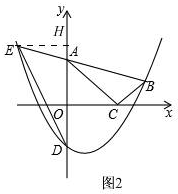 ��3����ͼ2������E��EH��y�ᣬ����ΪH��
��3����ͼ2������E��EH��y�ᣬ����ΪH��
�������㷨����ֱ��AB�Ľ���ʽ��y=-$\frac{\sqrt{3}}{3}$x+$\sqrt{3}$��
����$\left\{\begin{array}{l}{y=-\frac{\sqrt{3}}{3}x+\sqrt{3}}\\{y=\frac{\sqrt{3}}{3}{x}^{2}-\frac{\sqrt{3}}{3}x-\frac{\sqrt{3}}{3}}\end{array}\right.$��
��ã�x=-2����x=2����ȥ����
��ʱy=$\frac{5\sqrt{3}}{3}$��
��AE=2��OA=$\frac{5\sqrt{3}}{3}$��
y=$\frac{\sqrt{3}}{3}$x2-$\frac{\sqrt{3}}{3}$x-$\frac{\sqrt{3}}{3}$����x=0ʱ��y=-$\frac{\sqrt{3}}{3}$��
��D��0��-$\frac{\sqrt{3}}{3}$����
��HD=2$\sqrt{3}$��
��tan��ADE=tan��CAO=$\frac{\sqrt{3}}{3}$��
���ADE=��CAO��
��ED��AC��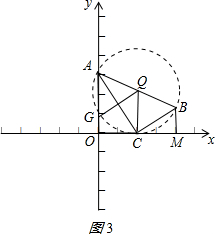
��4��$\frac{2\sqrt{3}��}{9}$
������ͼ��ͼ3������ABΪֱ����ԲQ������QC��
�������֪��P��O��C��Ӧ��F���˶��켣����ABΪֱ����Բ�ϵĻ�GC��
��A��0��$\sqrt{3}$����B��2��$\frac{\sqrt{3}}{3}$������Բ��Q��1��$\frac{2\sqrt{3}}{3}$����QC=$\frac{2\sqrt{3}}{3}$��
��C��1��0����
�����GQC=60�㣬
���Ի�GC=$\frac{60���С�\frac{2\sqrt{3}}{3}}{180}$=$\frac{2\sqrt{3}��}{9}$��
���� ���⿼����κ������ۺ����⣬���������ߺ�ֱ�ߵĽ���ʽ�����������ߺ�ֱ�ߵĽ��㣬��������ֱ�ߵĶԳƵ�����꣬�ܸ��������жϵ���˶��켣�ǽ���Ĺؼ���

 �������¿��ÿ�ʱ��ҵϵ�д�
�������¿��ÿ�ʱ��ҵϵ�д� Ӣ�żƻ�ͬ����ʱ��Чѵ��ϵ�д�
Ӣ�żƻ�ͬ����ʱ��Чѵ��ϵ�д��ף�$\frac{x-y}{\sqrt{x}+\sqrt{y}}$=$\frac{��x-y����\sqrt{x}-\sqrt{y}��}{��\sqrt{x}+\sqrt{y}����\sqrt{x}-\sqrt{y}��}$=$\sqrt{x}$-$\sqrt{y}$��
�ң�$\frac{x-y}{\sqrt{x}+\sqrt{y}}$=$\frac{��\sqrt{x}+\sqrt{y}����\sqrt{x}-\sqrt{y}��}{\sqrt{x}+\sqrt{y}}$=$\sqrt{x}$-$\sqrt{y}$��
���ڼס�����λͬѧ�Ľⷨ����ȷ���ж��ǣ�������
| A�� | �ס��Ҷ���ȷ | B�� | ����ȷ���Ҳ���ȷ | C�� | �ס��Ҷ�����ȷ | D�� | ����ȷ���ײ���ȷ |
| A�� | 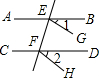 | B�� | 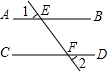 | C�� | 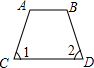 | D�� | 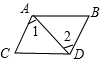 |
 ��ͼ����ƽ��ֱ������ϵ�У���������y=a��x+1��2-2��x��0��aΪ�������Ķ���A��AB��x���ڵ�B����������y=-a��x-1��2+2��x��0��aΪ�������Ķ���C��CD��x���ڵ�D������AD��BC�����ı���ABCD�����Ϊ4��
��ͼ����ƽ��ֱ������ϵ�У���������y=a��x+1��2-2��x��0��aΪ�������Ķ���A��AB��x���ڵ�B����������y=-a��x-1��2+2��x��0��aΪ�������Ķ���C��CD��x���ڵ�D������AD��BC�����ı���ABCD�����Ϊ4��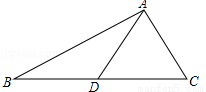
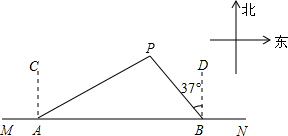 ��ͼ����A��B�ڶ�������ĺ�����MN�ϣ����յ��Ѵ�����dz�Ĵ�P������źţ���֪��P�ڴ�A�ı�ƫ��62�㷽���ϣ��ڴ�B�ı�ƫ��37�㷽���ϣ���AP=30�����B����P�ľ���PB������ú�������ǵ����Ǻ�����ʾ���ɣ���
��ͼ����A��B�ڶ�������ĺ�����MN�ϣ����յ��Ѵ�����dz�Ĵ�P������źţ���֪��P�ڴ�A�ı�ƫ��62�㷽���ϣ��ڴ�B�ı�ƫ��37�㷽���ϣ���AP=30�����B����P�ľ���PB������ú�������ǵ����Ǻ�����ʾ���ɣ���