题目内容
20.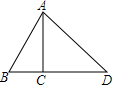 如图,AC是△ABC的高,AB=4,∠BAC=30°,∠DAC=45°,求AD.
如图,AC是△ABC的高,AB=4,∠BAC=30°,∠DAC=45°,求AD.
分析 首先在直角三角形BCA中利用AB和∠BAC的度数求得AC的长,然后利用等腰直角三角形的性质得到AC=CD,利用勾股定理求得AC的长即可.
解答 解:∵AC是△ABC的高,
∴∠ACB=∠ACD=90°,
∵AB=4,∠BAC=30°,
∴AC=ABcos∠BAC=4×$\frac{\sqrt{3}}{2}$=2$\sqrt{3}$,
∵∠DAC=45°,
∴AC=CD=2$\sqrt{3}$,
∴AD=$\sqrt{A{C}^{2}+C{D}^{2}}$=2$\sqrt{6}$.
点评 本题考查了勾股定理的运用,考查了含30°角直角三角形中斜边长为30°角所对直角边一半的性质,考查了等腰直角三角形腰长相等的性质.

练习册系列答案
 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案
相关题目
11.某种服装进价120元,在试销阶段发现每件售价(元)与产品的日销量(件)始终存在下表中的数量关系:
(1)根据上表所给的数据可知表中的a值是1件.
(2)在不改变上述关系的情况下,当每件定价为多少元时日盈利可达1600元?
| 每件售价(元) | 130 | 150 | 165 | 199 |
| 每日销售量(件) | 70 | 50 | 35 | a |
(2)在不改变上述关系的情况下,当每件定价为多少元时日盈利可达1600元?
10.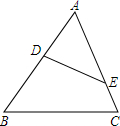 如图,在△ABC中,∠ADE=∠C,那么下列等式中,成立的是( )
如图,在△ABC中,∠ADE=∠C,那么下列等式中,成立的是( )
 如图,在△ABC中,∠ADE=∠C,那么下列等式中,成立的是( )
如图,在△ABC中,∠ADE=∠C,那么下列等式中,成立的是( )| A. | $\frac{DE}{BC}$=$\frac{AE}{AB}$ | B. | $\frac{AE}{BC}$=$\frac{AD}{BD}$ | C. | $\frac{AD}{AB}$=$\frac{AE}{AC}$ | D. | $\frac{DE}{BC}$=$\frac{AD}{AB}$ |
 如图,DE与BC不平行,请添加一个条件:∠ADE=∠C(答案不唯一),使△ADE∽△ACB.
如图,DE与BC不平行,请添加一个条件:∠ADE=∠C(答案不唯一),使△ADE∽△ACB.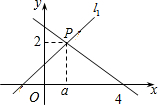 如图,直线l1:y1=x+1与直线l2:y2=mx+n相交于点P(a,2).
如图,直线l1:y1=x+1与直线l2:y2=mx+n相交于点P(a,2).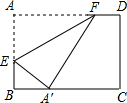 如图,长方形ABCD中,AD=10,AB=8,将长方形ABCD折叠,折痕为EF,点A的对应点A′落在线段BC上,当点A′在BC上移动时,点E、F也随之移动,若限定点E、F分别在线段AB、AD上移动,则点A′在线段BC上可移动的最大距离是4.
如图,长方形ABCD中,AD=10,AB=8,将长方形ABCD折叠,折痕为EF,点A的对应点A′落在线段BC上,当点A′在BC上移动时,点E、F也随之移动,若限定点E、F分别在线段AB、AD上移动,则点A′在线段BC上可移动的最大距离是4.