题目内容
8．电子跳蚤落在数轴上的某点K0，第一步从K0向左跳1个单位到K1，第二步由K1向右跳2个单位到K2，第三步由K2向左跳3个单位到K3，第四步由K3跳4个单位到K4，…，按以上规律跳了100步时，电子跳蚤落在数轴上的点K100所表示的数恰是20，试求电子跳蚤的初始位置K0点所表示的数．分析 易得每跳动2次，向右平移1个单位，跳动100次，相当于在原数的基础上加了50，相应的等量关系为：原数字+50=20．
解答 解：设k0点所对应的数为x，
由题意得：每跳动2次，向右平移1个单位，跳动100次，相当于在原数的基础上加了50，
则x+50=20，
解得：x=-30．
即电子跳蚤的初始位置K0点所表示的数为-30．
点评 本题考查了数轴、图形的变化规律；得到每跳动2次相对于原数的规律是解决本题的突破点．
练习册系列答案
相关题目
18．已知一元二次方程2x2+x-5=0的两根分别是x1，x2，则x12+x22的值是（ ）
| A． | $\frac{1}{2}$ | B． | -$\frac{1}{2}$ | C． | -$\frac{21}{4}$ | D． | $\frac{21}{4}$ |
16．
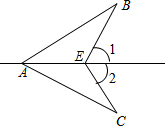如图，∠1=∠2，要使△ABE≌△ACE，还需添加一个条件不能是（ ）
如图，∠1=∠2，要使△ABE≌△ACE，还需添加一个条件不能是（ ）| A． | BE=CE | B． | ∠B=∠C | C． | AB=AC | D． | ∠BAE=∠CAE |
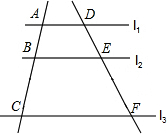如图，l1∥l2∥l3，直线a、b与l1、l2、l3分别相交于点A、B、C和点D、E、F，若AB=1，DE=2，DF=8，则BC的长为（ ）
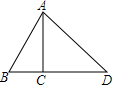如图，AC是△ABC的高，AB=4，∠BAC=30°，∠DAC=45°，求AD．
如图，△ABC中，∠C=90°，AD是∠CAB的角平分线，∠ADC=60°，求∠B的度数．