题目内容
11.某种服装进价120元,在试销阶段发现每件售价(元)与产品的日销量(件)始终存在下表中的数量关系:| 每件售价(元) | 130 | 150 | 165 | 199 |
| 每日销售量(件) | 70 | 50 | 35 | a |
(2)在不改变上述关系的情况下,当每件定价为多少元时日盈利可达1600元?
分析 (1)根据表格中的数据可得,售价每增长1元,日销量就降低1件,据此可得a=1;
(2)设每件定价为x元时日盈利可达1600元,则此时日销量为[80-(x-120)],据此列方程求解.
解答 解:(1)由表格可得:a=1;
故答案为:1.
(2)设每件定价为x元,则此时日销量为[80-(x-120)],
由题意得,(x-120)[80-(x-120)]=1600,
解得:x=160.
答:当每件定价为160元时日盈利可达1600元.
点评 本题考查了一元二次方程的应用,解答本题的关键是读懂题意,设出未知数,找出合适的等量关系,列方程求解.

练习册系列答案
相关题目
16.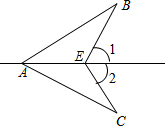 如图,∠1=∠2,要使△ABE≌△ACE,还需添加一个条件不能是( )
如图,∠1=∠2,要使△ABE≌△ACE,还需添加一个条件不能是( )
 如图,∠1=∠2,要使△ABE≌△ACE,还需添加一个条件不能是( )
如图,∠1=∠2,要使△ABE≌△ACE,还需添加一个条件不能是( )| A. | BE=CE | B. | ∠B=∠C | C. | AB=AC | D. | ∠BAE=∠CAE |
1.若A是三次多项式,B是二次多项式,则A+B一定是( )
| A. | 五次多项式 | B. | 三次多项式 | C. | 三次单项式 | D. | 三次的整式 |
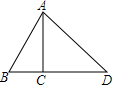 如图,AC是△ABC的高,AB=4,∠BAC=30°,∠DAC=45°,求AD.
如图,AC是△ABC的高,AB=4,∠BAC=30°,∠DAC=45°,求AD.