题目内容
12．
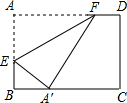如图，长方形ABCD中，AD=10，AB=8，将长方形ABCD折叠，折痕为EF，点A的对应点A′落在线段BC上，当点A′在BC上移动时，点E、F也随之移动，若限定点E、F分别在线段AB、AD上移动，则点A′在线段BC上可移动的最大距离是4．
分析 根据翻折变换，当点F与点D重合时，点A′到达最左边，当点E与点B重合时，点A′到达最右边，所以点A′就在这两个点之间移动，分别求出这两个位置时A′C的长度，然后两数相减就是最大距离．
解答 解：如图1所示：
当点F与点D重合时，根据翻折对称性可得：DA′=DA=10，
在Rt△A′CD中，A′D2=A′C2+CD2，
即102=A′C2+82，
解得A′C=6．
如图2所示：
当点E与点B重合时，根据翻折对称性可得BA′=AB=8．
∵A′C=CB-BA′，
∴A′C=2．
∴点E在BC边上可移动的最大距离为6-2=4=4．
故答案为：4．
点评 本题考查的是翻折变换及勾股定理，熟知图形翻折不变性的性质是解答此题的关键．
练习册系列答案
相关题目
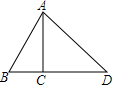如图，AC是△ABC的高，AB=4，∠BAC=30°，∠DAC=45°，求AD．
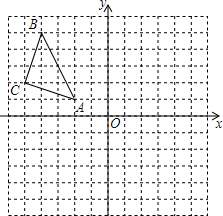如图，△ABC在平面直角坐标系中，点A、B、C的坐标分别为A（-2，1），B（-4，5），C（-5，2）．
1．若A是三次多项式，B是二次多项式，则A+B一定是（ ）
| A． | 五次多项式 | B． | 三次多项式 | C． | 三次单项式 | D． | 三次的整式 |
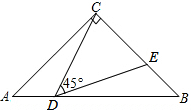如图，在Rt△ABC中，∠ACB=90°，CA=CB，AB=8．点D在边AB上（点D不与点A、B重合），连接CD，作∠CDE=45°，DE与边BC交于点E．