题目内容
5.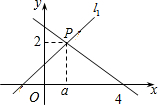 如图,直线l1:y1=x+1与直线l2:y2=mx+n相交于点P(a,2).
如图,直线l1:y1=x+1与直线l2:y2=mx+n相交于点P(a,2).(1)求a的值;
(2)求直线l2的解析式;
(3)写出y1>y2>0时,x的取值范围.
分析 (1)把点P(a,2)代入y1=x+1得到2=a+1,解方程即可求得;
(2)根据待定系数法即可求得;
(3)根据图象求得即可.
解答 解:(1)把点P(a,2)代入y1=x+1得,2=a+1,
解得a=1;
(2)把(1,2),(4,0)代入y2=mx+n得
$\left\{\begin{array}{l}{m+n=2}\\{4m+n=0}\end{array}\right.$,
解得$\left\{\begin{array}{l}{m=-\frac{2}{3}}\\{n=\frac{8}{3}}\end{array}\right.$.
所以直线l2的解析式为y2=-$\frac{2}{3}$x+$\frac{8}{3}$;
(3)由图象可知:y1>y2>0时,x的取值范围是1<x<4.
点评 本题考查了两条直线相交或平行问题以及待定系数法求一次函数的解析式,两条直线的交点坐标,符合这两条直线相对应的一次函数表达式是本题的关键.

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案 应用题作业本系列答案
应用题作业本系列答案
相关题目
15.以下列各组线段为边作三角形,能构成直角三角形的是( )
| A. | 6,5,4 | B. | 1,$\sqrt{2}$,$\sqrt{3}$ | C. | 4,19,20 | D. | 5,8,10 |
16.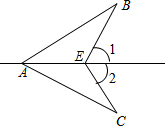 如图,∠1=∠2,要使△ABE≌△ACE,还需添加一个条件不能是( )
如图,∠1=∠2,要使△ABE≌△ACE,还需添加一个条件不能是( )
 如图,∠1=∠2,要使△ABE≌△ACE,还需添加一个条件不能是( )
如图,∠1=∠2,要使△ABE≌△ACE,还需添加一个条件不能是( )| A. | BE=CE | B. | ∠B=∠C | C. | AB=AC | D. | ∠BAE=∠CAE |
10.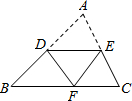 如图,D是AB的中点,将△ABC沿过D的直线折叠,使点A落在BC上的点F处,若∠B=46°,则∠BDF的度数是( )
如图,D是AB的中点,将△ABC沿过D的直线折叠,使点A落在BC上的点F处,若∠B=46°,则∠BDF的度数是( )
 如图,D是AB的中点,将△ABC沿过D的直线折叠,使点A落在BC上的点F处,若∠B=46°,则∠BDF的度数是( )
如图,D是AB的中点,将△ABC沿过D的直线折叠,使点A落在BC上的点F处,若∠B=46°,则∠BDF的度数是( )| A. | 80° | B. | 88° | C. | 92° | D. | 98° |
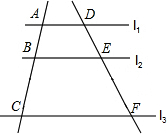 如图,l1∥l2∥l3,直线a、b与l1、l2、l3分别相交于点A、B、C和点D、E、F,若AB=1,DE=2,DF=8,则BC的长为( )
如图,l1∥l2∥l3,直线a、b与l1、l2、l3分别相交于点A、B、C和点D、E、F,若AB=1,DE=2,DF=8,则BC的长为( )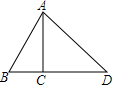 如图,AC是△ABC的高,AB=4,∠BAC=30°,∠DAC=45°,求AD.
如图,AC是△ABC的高,AB=4,∠BAC=30°,∠DAC=45°,求AD.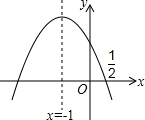 如图,抛物线y=ax2+bx+c的对称轴是x=-1.且过点($\frac{1}{2}$,0),有下列结论:①abc>0;②a-2b+4c=0;③25a-10b+4c=0;④3b+2c>0;⑤a-b≥m(am-b);其中正确的结论有( )
如图,抛物线y=ax2+bx+c的对称轴是x=-1.且过点($\frac{1}{2}$,0),有下列结论:①abc>0;②a-2b+4c=0;③25a-10b+4c=0;④3b+2c>0;⑤a-b≥m(am-b);其中正确的结论有( )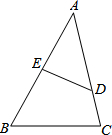 如图,在△ABC中,点D、E分别在边AC、AB上,且$\frac{AE}{AC}$=$\frac{AD}{AB}$=$\frac{2}{3}$,若DE=4,则BC=6.
如图,在△ABC中,点D、E分别在边AC、AB上,且$\frac{AE}{AC}$=$\frac{AD}{AB}$=$\frac{2}{3}$,若DE=4,则BC=6.