题目内容
14.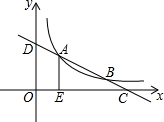 如图,已知直线y=-$\frac{1}{2}$x+m与反比例函数y=$\frac{k}{x}$的图象在第一象限内交于A,B两点(点A在点B的左侧),分别与x,y轴交于点C,D,AE⊥x轴于E.若OE•CE=12,则k的值是6.
如图,已知直线y=-$\frac{1}{2}$x+m与反比例函数y=$\frac{k}{x}$的图象在第一象限内交于A,B两点(点A在点B的左侧),分别与x,y轴交于点C,D,AE⊥x轴于E.若OE•CE=12,则k的值是6.
分析 首先证明$\frac{AE}{EC}$=$\frac{DO}{OC}$=$\frac{1}{2}$,设点A(a,b),则AE=b,OE=a,EC=2b,由OE•EC=12,得2ab=12,所以ab=6,由此即可解决问题.
解答 解:∵直线y=-$\frac{1}{2}$x+m 与x轴交于点C,与y轴交于点D,
与x轴交于点C,与y轴交于点D,
∴D(0,m),C(2m,0),
∴OC=2m,OD=m,
∵AE∥OD,
∴$\frac{AE}{DO}$=$\frac{CE}{OC}$,
∴$\frac{AE}{EC}$=$\frac{DO}{OC}$=$\frac{1}{2}$,
设点A(a,b),则AE=b,OE=a,EC=2b,
∵OE•EC=12,
∴2ab=12,
∴ab=6,
∴k=ab=6,
故答案为6.
点评 本题考查一次函数与反比例函数图象的解得问题,解题的关键是证明EC=2AE,学会利用参数解决问题,属于中考常考题型.

练习册系列答案
相关题目
4.将下列多项式因式分解,结果中不含有因式a+1的是( )
| A. | a2-1 | B. | a2+a | C. | a2+a-2 | D. | (a+2)2-2(a+2)+1 |
5.当a=$\sqrt{2}+1,b=\sqrt{2}$-1时,代数式$\frac{{{a^2}-2ab+{b^2}}}{{{a^2}-{b^2}}}$的值是$\frac{\sqrt{2}}{2}$.
2.在平面直角坐标系中点P(-2,3)和Q(m,n)关于x轴对称,则m的值为( )
| A. | m=-2 | B. | m=2 | C. | m=-3 | D. | m=3 |
19.某校要从甲、乙、丙、丁四名学生中选一名参加“汉字听写”大赛,选拔中每名学生的平均成绩$\overline{x}$及其方差s2如表所示,如果要选拔一名成绩高且发挥稳定的学生参赛,则应选择的学生是( )
| 甲 | 乙 | 丙 | 丁 | |
| $\overline{x}$ | 8.9 | 9.5 | 9.5 | 8.9 |
| s2 | 0.92 | 0.92 | 1.01 | 1.03 |
| A. | 甲 | B. | 乙 | C. | 丙 | D. | 丁 |
2.在解方程组$\left\{\begin{array}{l}{3x+2y=2①}\\{2x+2y=-1②}\end{array}\right.$中,①-②所得的方程是( )
| A. | x=1 | B. | 5x=-1 | C. | x=3 | D. | 5x=3 |