题目内容
5.当a=$\sqrt{2}+1,b=\sqrt{2}$-1时,代数式$\frac{{{a^2}-2ab+{b^2}}}{{{a^2}-{b^2}}}$的值是$\frac{\sqrt{2}}{2}$.分析 根据已知条件先求出a+b和a-b的值,再把要求的式子进行化简,然后代值计算即可.
解答 解:∵a=$\sqrt{2}+1,b=\sqrt{2}$-1,
∴a+b=$\sqrt{2}$+1+$\sqrt{2}$-1=2$\sqrt{2}$,a-b=$\sqrt{2}$+1-$\sqrt{2}$+1=2,
∴$\frac{{{a^2}-2ab+{b^2}}}{{{a^2}-{b^2}}}$=$\frac{(a-b)^{2}}{(a+b)(a-b)}$=$\frac{a-b}{a+b}$=$\frac{2}{2\sqrt{2}}$=$\frac{\sqrt{2}}{2}$;
故答案为:$\frac{\sqrt{2}}{2}$.
点评 此题考查了分式的值,用到的知识点是完全平方公式、平方差公式和分式的化简,关键是对给出的式子进行化简.

练习册系列答案
 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案
相关题目
13.己知P是线段AB上一点(与端点A、B不重合),M是线段AP的中点,N是线段BP中点,AB=6厘米,那么MN的长等于( )
| A. | 2厘米 | B. | 3厘米 | C. | 4厘米 | D. | 5厘米 |
17.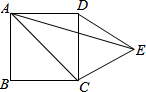 如图,在正方形ABCD的外侧,作等边三角形DCE,若∠AED=15°,则∠EAC=( )
如图,在正方形ABCD的外侧,作等边三角形DCE,若∠AED=15°,则∠EAC=( )
 如图,在正方形ABCD的外侧,作等边三角形DCE,若∠AED=15°,则∠EAC=( )
如图,在正方形ABCD的外侧,作等边三角形DCE,若∠AED=15°,则∠EAC=( )| A. | 15° | B. | 28° | C. | 30° | D. | 45° |
13.弹簧挂上物体后会伸长,已知一弹簧的长度(cm)与所挂物体的质量(kg)之间的关系如下表:
(1)如果物体的质量为x kg,弹簧长度为y cm,根据上表写出y与x的关系式;
(2)当物体的质量为2.5kg时,根据(1)的关系式,求弹簧的长度;
(3)当弹簧的长度为17cm时,根据(1)的关系式,求弹簧所挂物体的质量.
| 所挂物体的质量(kg) | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 弹簧的长度(cm) | 12 | 12.5 | 13 | 13.5 | 14 | 14.5 | 15 | 15.5 |
(2)当物体的质量为2.5kg时,根据(1)的关系式,求弹簧的长度;
(3)当弹簧的长度为17cm时,根据(1)的关系式,求弹簧所挂物体的质量.
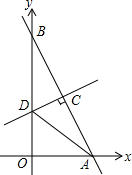 如图,在平面直角坐标系中,点A,B分别在x轴正半轴与y轴正半轴上,线段OA,OB(OA<OB)的长是方程x(x-4)+8(4-x)=0的两个根,作线段AB的垂直平分线交y轴于点D,交AB于点C.
如图,在平面直角坐标系中,点A,B分别在x轴正半轴与y轴正半轴上,线段OA,OB(OA<OB)的长是方程x(x-4)+8(4-x)=0的两个根,作线段AB的垂直平分线交y轴于点D,交AB于点C.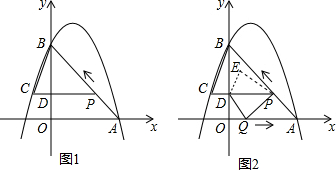

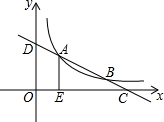 如图,已知直线y=-$\frac{1}{2}$x+m与反比例函数y=$\frac{k}{x}$的图象在第一象限内交于A,B两点(点A在点B的左侧),分别与x,y轴交于点C,D,AE⊥x轴于E.若OE•CE=12,则k的值是6.
如图,已知直线y=-$\frac{1}{2}$x+m与反比例函数y=$\frac{k}{x}$的图象在第一象限内交于A,B两点(点A在点B的左侧),分别与x,y轴交于点C,D,AE⊥x轴于E.若OE•CE=12,则k的值是6.