题目内容
6.化简求值:($\frac{a}{a+2}+\frac{1}{{a}^{2}-4}$)$÷\frac{a-1}{a+2}$$+\frac{1}{a-2}$,其中a=2+$\sqrt{2}$.分析 原式第一项括号中两项通分并利用同分母分式的加法法则计算,同时利用除法法则变形,约分后两项化简得到最简结果,把a的值代入计算即可求出值.
解答 解:原式=[$\frac{a(a-2)}{(a+2)(a-2)}$+$\frac{1}{(a+2)(a-2)}$]•$\frac{a+2}{a-1}$+$\frac{1}{a-2}$=$\frac{(a-1)^{2}}{(a+2)(a-2)}$•$\frac{a+2}{a-1}$+$\frac{1}{a-2}$=$\frac{a-1+1}{a-2}$=$\frac{a}{a-2}$,
当a=2+$\sqrt{2}$时,原式=$\sqrt{2}$+1.
点评 此题考查了分式的混合运算,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
17.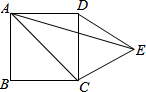 如图,在正方形ABCD的外侧,作等边三角形DCE,若∠AED=15°,则∠EAC=( )
如图,在正方形ABCD的外侧,作等边三角形DCE,若∠AED=15°,则∠EAC=( )
 如图,在正方形ABCD的外侧,作等边三角形DCE,若∠AED=15°,则∠EAC=( )
如图,在正方形ABCD的外侧,作等边三角形DCE,若∠AED=15°,则∠EAC=( )| A. | 15° | B. | 28° | C. | 30° | D. | 45° |
11.分解因式:16-x2=( )
| A. | (4-x)(4+x) | B. | (x-4)(x+4) | C. | (8+x)(8-x) | D. | (4-x)2 |
13.弹簧挂上物体后会伸长,已知一弹簧的长度(cm)与所挂物体的质量(kg)之间的关系如下表:
(1)如果物体的质量为x kg,弹簧长度为y cm,根据上表写出y与x的关系式;
(2)当物体的质量为2.5kg时,根据(1)的关系式,求弹簧的长度;
(3)当弹簧的长度为17cm时,根据(1)的关系式,求弹簧所挂物体的质量.
| 所挂物体的质量(kg) | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 弹簧的长度(cm) | 12 | 12.5 | 13 | 13.5 | 14 | 14.5 | 15 | 15.5 |
(2)当物体的质量为2.5kg时,根据(1)的关系式,求弹簧的长度;
(3)当弹簧的长度为17cm时,根据(1)的关系式,求弹簧所挂物体的质量.
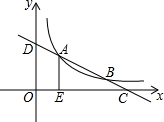 如图,已知直线y=-$\frac{1}{2}$x+m与反比例函数y=$\frac{k}{x}$的图象在第一象限内交于A,B两点(点A在点B的左侧),分别与x,y轴交于点C,D,AE⊥x轴于E.若OE•CE=12,则k的值是6.
如图,已知直线y=-$\frac{1}{2}$x+m与反比例函数y=$\frac{k}{x}$的图象在第一象限内交于A,B两点(点A在点B的左侧),分别与x,y轴交于点C,D,AE⊥x轴于E.若OE•CE=12,则k的值是6.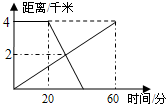 已知A、B两地相距4km,上午8:00时,亮亮从A地步行到B地,8:20时芳芳从B地出发骑自行车到A地,亮亮和芳芳两人离A地的距离S(km)与亮亮所用时间t(min)之间的函数关系如图所示,下列四个说法中正确的有( )
已知A、B两地相距4km,上午8:00时,亮亮从A地步行到B地,8:20时芳芳从B地出发骑自行车到A地,亮亮和芳芳两人离A地的距离S(km)与亮亮所用时间t(min)之间的函数关系如图所示,下列四个说法中正确的有( )