题目内容
1.计算:(-2)3-32+|$\sqrt{3}$-10|,其中$\sqrt{3}$=1.732.(结果精确到0.01)分析 分别利用绝对值的性质以及有理数的乘方运算法则分别化简求出答案.
解答 解:原式=-8-9+10-$\sqrt{3}$
=-7-$\sqrt{3}$
≈-7-1.732
≈-8.73.
点评 此题主要考查了绝对值的性质以及有理数的乘方运算等知识,正确化简各数是解题关键.

练习册系列答案
相关题目
13.己知P是线段AB上一点(与端点A、B不重合),M是线段AP的中点,N是线段BP中点,AB=6厘米,那么MN的长等于( )
| A. | 2厘米 | B. | 3厘米 | C. | 4厘米 | D. | 5厘米 |
11.分解因式:16-x2=( )
| A. | (4-x)(4+x) | B. | (x-4)(x+4) | C. | (8+x)(8-x) | D. | (4-x)2 |
13.弹簧挂上物体后会伸长,已知一弹簧的长度(cm)与所挂物体的质量(kg)之间的关系如下表:
(1)如果物体的质量为x kg,弹簧长度为y cm,根据上表写出y与x的关系式;
(2)当物体的质量为2.5kg时,根据(1)的关系式,求弹簧的长度;
(3)当弹簧的长度为17cm时,根据(1)的关系式,求弹簧所挂物体的质量.
| 所挂物体的质量(kg) | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 弹簧的长度(cm) | 12 | 12.5 | 13 | 13.5 | 14 | 14.5 | 15 | 15.5 |
(2)当物体的质量为2.5kg时,根据(1)的关系式,求弹簧的长度;
(3)当弹簧的长度为17cm时,根据(1)的关系式,求弹簧所挂物体的质量.
10.一艘轮船在静水中的最大航速为30km/h,它以最大航速沿江顺流航行90km所用时间,与以最大航速逆流航行60km所用时间相等.设江水的流速为vkm/h,根据题意,下列所列方程正确的是( )
| A. | $\frac{90}{30+v}=\frac{60}{30-v}$ | B. | $\frac{90}{v}=\frac{60}{30-v}$ | C. | $\frac{90}{30-v}=\frac{60}{30+v}$ | D. | $\frac{90}{30-v}=\frac{60}{v}$ |
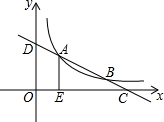 如图,已知直线y=-$\frac{1}{2}$x+m与反比例函数y=$\frac{k}{x}$的图象在第一象限内交于A,B两点(点A在点B的左侧),分别与x,y轴交于点C,D,AE⊥x轴于E.若OE•CE=12,则k的值是6.
如图,已知直线y=-$\frac{1}{2}$x+m与反比例函数y=$\frac{k}{x}$的图象在第一象限内交于A,B两点(点A在点B的左侧),分别与x,y轴交于点C,D,AE⊥x轴于E.若OE•CE=12,则k的值是6.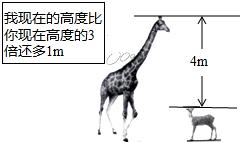 如图,根据图中的信息,若设长颈鹿的身高为xm,梅花鹿的身高为ym,则可列方程组$\left\{\begin{array}{l}{x-y=4}\\{x=3y+1}\end{array}\right.$.
如图,根据图中的信息,若设长颈鹿的身高为xm,梅花鹿的身高为ym,则可列方程组$\left\{\begin{array}{l}{x-y=4}\\{x=3y+1}\end{array}\right.$.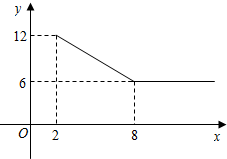 某公司经营杨梅业务,以3万元/吨的价格买入杨梅后,分拣成A、B两类,A类杨梅包装后直接销售,包装成本为1万元/吨,它的平均销售价格y(单位:万元/吨)与销售数量x(x≥2,单位:吨)之间的函数关系如图所示;B类杨梅深加工后再销售,深加工总费用s(单位:万元)与加工数量t(单位:吨)之间的函数关系是s=12+3t,平均销售价格为9万元/吨.
某公司经营杨梅业务,以3万元/吨的价格买入杨梅后,分拣成A、B两类,A类杨梅包装后直接销售,包装成本为1万元/吨,它的平均销售价格y(单位:万元/吨)与销售数量x(x≥2,单位:吨)之间的函数关系如图所示;B类杨梅深加工后再销售,深加工总费用s(单位:万元)与加工数量t(单位:吨)之间的函数关系是s=12+3t,平均销售价格为9万元/吨.