Question

6．如图，是某广场台阶（结合轮椅专用坡道）景观设计的模型，以及该设计第一层的截面图，第一层有十级台阶，每级台阶的高为0.15米，宽为0.4米，轮椅专用坡道AB的顶端有一个宽2米的水平面BC；《城市道路与建筑物无障碍设计规范》第17条，新建轮椅专用坡道在不同坡度的情况下，坡道高度应符合以下表中的规定：

坡度	1：20	1：16	1：12
最大高度（米）	1.50	1.00	0.75

（1）选择哪个坡度建设轮椅专用坡道AB是符合要求的？说明理由；
（2）求斜坡底部点A与台阶底部点D的水平距离AD．

Answer 1

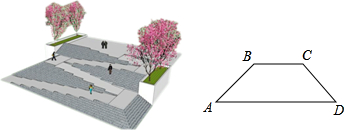
分析 （1）计算最大高度为：0.15×10=1.5（米），由表格查对应的坡度为：1：20；
（2）作梯形的高BE、CF，由坡度计算AE的长，由台阶的宽计算DF的长，相加可得AD的长．

解答 解：（1）∵第一层有十级台阶，每级台阶的高为0.15米，
∴最大高度为0.15×10=1.5（米），
由表知建设轮椅专用坡道AB选择符合要求的坡度是1：20；
（2）如图，过B作BE⊥AD于E，过C作CF⊥AD于F，

∴BE=CF=1.5，EF=BC=2，
∵$\frac{BE}{AE}$=$\frac{1}{20}$，
∴$\frac{1.5}{AE}$=$\frac{1}{20}$，
∴AE=30，
∵DF=9×0.4=3.6
∴AD=AE+EF+DF=30+2+3.6=35.6，
答：斜坡底部点A与台阶底部点D的水平距离AD为35.6米．

点评 本题考查了坡度坡角问题，在解决坡度的有关问题中，一般通过作高构成直角三角形，坡角即是一锐角，坡度实际就是一锐角的正切值，利用三角函数的定义列等式即可．