题目内容
7.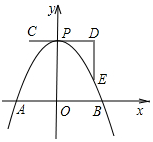 如图,一条抛物线与x轴的交点为A、B两点,其顶点P在折线C-D-E上运动.若C、D、E的坐标分别为(-1,4)、(3、4)、(3,1),点B横坐标的最小值为1,则点A横坐标的最大值为2.
如图,一条抛物线与x轴的交点为A、B两点,其顶点P在折线C-D-E上运动.若C、D、E的坐标分别为(-1,4)、(3、4)、(3,1),点B横坐标的最小值为1,则点A横坐标的最大值为2.
分析 抛物线在平移过程中形状没有发生变化,因此函数解析式的二次项系数在平移前后不会改变.首先,当点B横坐标取最小值时,函数的顶点在C点,根据待定系数法可确定抛物线的解析式;而点A横坐标取最大值时,抛物线的顶点应移动到E点,结合前面求出的二次项系数以及E点坐标可确定此时抛物线的解析式,进一步能求出此时点A的坐标,即点A的横坐标最大值.
解答 解:由图知:当点B的横坐标为1时,抛物线顶点取C(-1,4),
设该抛物线的解析式为:y=a(x+1)2+4,
代入点B坐标,得0=a(1+1)2+4,
解得:a=-1,
即:B点横坐标取最小值时,抛物线的解析式为:y=-(x+1)2+4.
当A点横坐标取最大值时,抛物线顶点应取E(3,1),
则此时抛物线的解析式:y=-(x-3)2+1=-x2+6x-8=-(x-2)(x-4),
即与x轴的交点为(2,0)或(4,0)(舍去),
故点A的横坐标的最大值为2.
故答案为2.
点评 此题考查了二次函数综合题,解答该题的关键在于读透题意,要注意的是抛物线在平移过程中形状并没有发生变化,改变的是顶点坐标.注意抛物线顶点所处的C、E两个关键位置,前者能确定函数解析式、后者能得到要求的结果.

练习册系列答案
相关题目
15.化简$\frac{{a-{a^2}b}}{{a-{b^{-1}}}}$结果是( )
| A. | -ab | B. | ab-1 | C. | ab | D. | ab3 |
2.已知x=1是一元二次方程x2+bx+1=0的解,则b的值为( )
| A. | 0 | B. | 1 | C. | -2 | D. | 2 |
19.把一张圆形纸片按如图方式折叠两次后展开,图中的虚线表示折痕,则∠BOC的度数是( )


| A. | 120° | B. | 135° | C. | 150° | D. | 165° |

 某中学课外兴趣活动小组准备围建一个矩形苗圃园,其中一边靠墙,另外三边周长为30米的篱笆围成.已知墙长为20米(如图所示),设这个苗圃园垂直于墙的一边长为x米
某中学课外兴趣活动小组准备围建一个矩形苗圃园,其中一边靠墙,另外三边周长为30米的篱笆围成.已知墙长为20米(如图所示),设这个苗圃园垂直于墙的一边长为x米 如图,?ABCD中,点E、F分别在边AD、BC上,且BE∥DF,若AE=3,则CF=3.
如图,?ABCD中,点E、F分别在边AD、BC上,且BE∥DF,若AE=3,则CF=3.