题目内容
10. 如图,在楼房底部B处看热气球底部A处的仰角为60°,同时在这栋楼的顶部C处看A处的仰角为30°,已知楼高BC为30m,求此时热气球底部A处的高度.(测角仪的高度忽略不计)
如图,在楼房底部B处看热气球底部A处的仰角为60°,同时在这栋楼的顶部C处看A处的仰角为30°,已知楼高BC为30m,求此时热气球底部A处的高度.(测角仪的高度忽略不计)
分析 作AD⊥BC交BC的延长线于点D,根据三角形的外角的性质得到∠BAC=30°,根据余弦的性质求出CD,计算即可.
解答 解:作AD⊥BC交BC的延长线于点D,
根据题意可知,∠ABD=30°,∠ACD=60°,
∴∠BAC=∠ACD-∠ABD=30°,
∴∠BAC=∠ABD,
∴AC=BC=30(m),
在Rt△ACD中,CD=AC•cos∠ACD=15(m),
∴BD=BC+CD=45(m),
此时热气球底部A处的高度为45m.
点评 本题考查的是解直角三角形的应用-仰角俯角问题,掌握仰角俯角的概念、熟记锐角三角函数的定义是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
20.计算sin60°•$\sqrt{3}$的值是( )
| A. | 1 | B. | $\frac{2}{3}$ | C. | $\frac{3}{2}$ | D. | 3 |
5.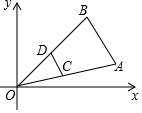 如图,线段AB两个端点的坐标分别为A(8,2),B (6,6),以原点O为位似中心,在第一象限内将线段AB缩小为原来的一半后得到线段CD,则端点C的坐标为( )
如图,线段AB两个端点的坐标分别为A(8,2),B (6,6),以原点O为位似中心,在第一象限内将线段AB缩小为原来的一半后得到线段CD,则端点C的坐标为( )
 如图,线段AB两个端点的坐标分别为A(8,2),B (6,6),以原点O为位似中心,在第一象限内将线段AB缩小为原来的一半后得到线段CD,则端点C的坐标为( )
如图,线段AB两个端点的坐标分别为A(8,2),B (6,6),以原点O为位似中心,在第一象限内将线段AB缩小为原来的一半后得到线段CD,则端点C的坐标为( )| A. | (3,3) | B. | (4,3) | C. | (3,1) | D. | (4,1) |
15.化简$\frac{{a-{a^2}b}}{{a-{b^{-1}}}}$结果是( )
| A. | -ab | B. | ab-1 | C. | ab | D. | ab3 |
2.已知x=1是一元二次方程x2+bx+1=0的解,则b的值为( )
| A. | 0 | B. | 1 | C. | -2 | D. | 2 |
19.把一张圆形纸片按如图方式折叠两次后展开,图中的虚线表示折痕,则∠BOC的度数是( )


| A. | 120° | B. | 135° | C. | 150° | D. | 165° |
