题目内容
6．在等腰△ABC中，AB=AC，BD⊥AC，∠ABC=70°，则∠ABD=（ ）| A． | 30° | B． | 40° | C． | 50° | D． | 60° |
分析 根据等腰三角形的性质由已知可求得∠A的度数，再根据垂直的定义和三角形内角和定理不难求得∠ABD的度数．
解答 解：∵AB=AC，∠ABC=70°，
∴∠ABC=∠ACB=70°，
∴∠A=40°，
∵BD⊥AC，
∴∠ABD=90°-40°=50°．
故选：C．
点评 本题主要考查等腰三角形的性质，解答本题的关键是会综合运用等腰三角形的性质和三角形的内角和定理进行答题，此题难度一般．
练习册系列答案
名校课堂系列答案
相关题目
11．要建一个长40米，宽20米的厂房，在比例尺是1：500的图纸上，长要画（ ）厘米．
| A． | 5 | B． | 8 | C． | 7 | D． | 6 |
18．
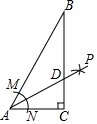如图，在△ABC中，∠C=90°，∠B=30°，以A为圆心，小于AC为半径画弧，分别交AB、AC于点M和N，再分别以M、N为圆心，大于$\frac{1}{2}$MN的长为半径画弧，两弧交于点P，连接AP交BC于点，则下列说法不正确的是（ ）
如图，在△ABC中，∠C=90°，∠B=30°，以A为圆心，小于AC为半径画弧，分别交AB、AC于点M和N，再分别以M、N为圆心，大于$\frac{1}{2}$MN的长为半径画弧，两弧交于点P，连接AP交BC于点，则下列说法不正确的是（ ）| A． | AD平分∠BAC | B． | S△DAC：S△ABC=1：2 | ||
| C． | 点D在线段AB的垂直平分线上 | D． | ∠ADC=60° |
16．下列各图中，∠1与∠2是对顶角的是（ ）
| A． |  | B． |  | C． |  | D． |  |