题目内容
12．求（x-1）（2x+1）-2（x-5）（x+2）的值，其中x=-2．分析 根据多项式乘多项式的运算法则把要求的式子进行整理，然后代值计算即可．
解答 解：（x-1）（2x+1）-2（x-5）（x+2）
=2x2-x-1-2（x2-3x-10）
=2x2-x-1-2x2+6x+20
=5x+19，
把x=-2代入原式得：
原式=5×（-2）+19=-10+19=9．
点评 此题考查了多项式乘多项式，掌握多项式乘多项式的运算法则是本题的关键，是一道基础题．
练习册系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
3．下列运算正确的是（ ）
| A． | $\sqrt{（-4）^2}$=±4 | B． | $\sqrt{\frac{1}{4}+\frac{1}{16}}$=$\frac{1}{2}$+$\frac{1}{4}$ | C． | -$\sqrt{-25}$=（-5）=5 | D． | $\sqrt{6^2+8^2}$=10 |
7．下列各式中无意义的是（ ）
| A． | $\root{3}{-2}$ | B． | $\root{3}{a}$ | C． | $\sqrt{-3}$ | D． | $\sqrt{{a}^{2}}$ |
2．
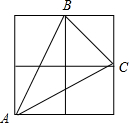如图，在2×2的网格中，有一个格点三角形△ABC，若每个小正方形的边长为1，则△ABC的边长BC边上的高为（ ）
如图，在2×2的网格中，有一个格点三角形△ABC，若每个小正方形的边长为1，则△ABC的边长BC边上的高为（ ）| A． | $\sqrt{5}$ | B． | 2$\sqrt{2}$ | C． | $\frac{3}{2}$$\sqrt{2}$ | D． | 2 |