题目内容
等腰三角形的一边长是8cm,另一边长是5cm,则这个等腰三角形的周长是 cm.
考点:等腰三角形的性质,三角形三边关系
专题:
分析:分5cm是腰长和底边两种情况,求出三角形的三边,再根据三角形的三边关系判定求解.
解答:解:①若5cm是腰长,则三角形的三边分别为5cm,5cm,8cm,
能组成三角形,
周长=5+5+8=18cm,
②若5cm是底边,则三角形的三边分别为5cm,8cm,8cm,
能组成三角形,
周长=5+8+8=21cm,
综上所述,这个等腰三角形的周长是18cm或21cm.
故答案为:18cm或21.
能组成三角形,
周长=5+5+8=18cm,
②若5cm是底边,则三角形的三边分别为5cm,8cm,8cm,
能组成三角形,
周长=5+8+8=21cm,
综上所述,这个等腰三角形的周长是18cm或21cm.
故答案为:18cm或21.
点评:本题考查了等腰三角形的性质,主要利用了等腰三角形两腰相等的性质,难点在于分情况讨论.

练习册系列答案
相关题目
以下列各组数为边的三角形不是直角三角形的是( )
| A、5,6,9 |
| B、5,3,4 |
| C、24,10,26 |
| D、60,11,61 |
对于函数y=3(x-2)2,下列说法正确的是( )
| A、当x>0时,y随x的增大而减小 |
| B、当x<0时,y随x的增大而增大 |
| C、当x>2时,y随x的增大而增大 |
| D、当x>-2时,y随x的增大而减小 |
在半径为10的⊙O中,弦AB=12,弦CD=16,且AB∥CD,则弦AB、CD的距离为( )
| A、14 | B、2 |
| C、8或6 | D、14或2 |
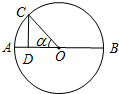 如图,AB为⊙O的直径,D为AB上一点,且AB=6AD,CD⊥AB于D,C在⊙O上,设∠COD=α,则tan
如图,AB为⊙O的直径,D为AB上一点,且AB=6AD,CD⊥AB于D,C在⊙O上,设∠COD=α,则tan| α |
| 2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
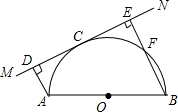 如图,已知AB为半圆O的直径,直线MN切半圆于点C,AD⊥MN于点D,BE⊥MN于点E,BE交半圆于点F,AD=3cm,BE=7cm.
如图,已知AB为半圆O的直径,直线MN切半圆于点C,AD⊥MN于点D,BE⊥MN于点E,BE交半圆于点F,AD=3cm,BE=7cm.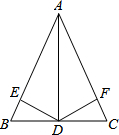 如图,在△ABC中,AD是边BC的垂直平分线,DE⊥AB于E,DF⊥AC于F.
如图,在△ABC中,AD是边BC的垂直平分线,DE⊥AB于E,DF⊥AC于F.