题目内容
18.先化简($\frac{3m+4}{{m}^{2}-1}$-$\frac{2}{m-1}$)÷$\frac{m+2}{{m}^{2}-2m+1}$,再从-2≤m≤1的取值范围内,选取一个你认为合适的m的整数值代入求值.分析 先化简题目中的式子,然后再从-2≤m≤1中,选取一个合适的m的整数值代入求值即可解答本题,注意m不等于-2、-1、1.
解答 解:($\frac{3m+4}{{m}^{2}-1}$-$\frac{2}{m-1}$)÷$\frac{m+2}{{m}^{2}-2m+1}$
=$\frac{3m+4-2(m+1)}{(m+1)(m-1)}×\frac{(m-1)^{2}}{m+2}$
=$\frac{m+2}{(m+1)(m-1)}×\frac{(m-1)^{2}}{m+2}$
=$\frac{m-1}{m+1}$,
当m=0时,原式=$\frac{0-1}{0+1}=-1$.
点评 本题考查分式的化简求值,解答本题的关键是明确分式化简求值的方法.

练习册系列答案
 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案
相关题目
8.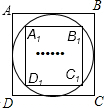 如图,我们把先作正方形ABCD的内切圆,再作这个内切圆的内接正方形A1B1C1D1.称为第一次数学操作,解下列,作正方形A1B1C1D1的内切圆,再作这个内切圆的内接正方形A2B2C2D2,称为第二次数学操作,按此规律如此下去,…,当完成第n次数学操作后,得到正方形AnBnCnDn,则$\frac{{A}_{n}{B}_{n}}{AB}$的值为( )
如图,我们把先作正方形ABCD的内切圆,再作这个内切圆的内接正方形A1B1C1D1.称为第一次数学操作,解下列,作正方形A1B1C1D1的内切圆,再作这个内切圆的内接正方形A2B2C2D2,称为第二次数学操作,按此规律如此下去,…,当完成第n次数学操作后,得到正方形AnBnCnDn,则$\frac{{A}_{n}{B}_{n}}{AB}$的值为( )
 如图,我们把先作正方形ABCD的内切圆,再作这个内切圆的内接正方形A1B1C1D1.称为第一次数学操作,解下列,作正方形A1B1C1D1的内切圆,再作这个内切圆的内接正方形A2B2C2D2,称为第二次数学操作,按此规律如此下去,…,当完成第n次数学操作后,得到正方形AnBnCnDn,则$\frac{{A}_{n}{B}_{n}}{AB}$的值为( )
如图,我们把先作正方形ABCD的内切圆,再作这个内切圆的内接正方形A1B1C1D1.称为第一次数学操作,解下列,作正方形A1B1C1D1的内切圆,再作这个内切圆的内接正方形A2B2C2D2,称为第二次数学操作,按此规律如此下去,…,当完成第n次数学操作后,得到正方形AnBnCnDn,则$\frac{{A}_{n}{B}_{n}}{AB}$的值为( )| A. | ($\frac{\sqrt{2}}{2}$)n | B. | ($\frac{1}{2}$)n | C. | ($\frac{\sqrt{3}}{2}$)n | D. | ($\frac{3}{4}$)n |
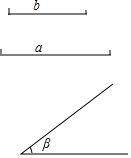 画△ABC,使其两边为已知线段a、b,夹角为β.(要求:用尺规作图,写出己知,求作;保留作图痕迹;不在已知的线、角上作图;不写作法).
画△ABC,使其两边为已知线段a、b,夹角为β.(要求:用尺规作图,写出己知,求作;保留作图痕迹;不在已知的线、角上作图;不写作法).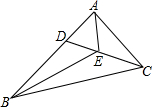 在△ABC中,点D为AB边上一点,BD=2AD,点E为CD的中点,若S△ADE=2,则S△ABC=12.
在△ABC中,点D为AB边上一点,BD=2AD,点E为CD的中点,若S△ADE=2,则S△ABC=12.