题目内容
9.先阅读下面的解题过程,然后再解答:形如$\sqrt{m±2\sqrt{n}}$的化简,只要我们找到两个数a,b,使a+b=m,ab=n,即${({\sqrt{a}})^2}+{({\sqrt{b}})^2}$=m,$\sqrt{a}•\sqrt{b}=\sqrt{n}$,那么便有:$\sqrt{m±2\sqrt{n}}=\sqrt{{{({\sqrt{a}±\sqrt{b}})}^2}}=\sqrt{a}±\sqrt{b}({a>b})$
根据上述方法化简:
(1)$\sqrt{13-2\sqrt{42}}$.
(2)$\sqrt{7+4\sqrt{3}}$.
分析 (1)直接利用完全平方公式化简求出答案;
(2)直接利用完全平方公式化简求出答案.
解答 解:(1)$\sqrt{13-2\sqrt{42}}$=$\sqrt{(\sqrt{6}-\sqrt{7})^{2}}$=$\sqrt{7}$-$\sqrt{6}$;
(2)$\sqrt{7+4\sqrt{3}}$=$\sqrt{(2+\sqrt{3})^{2}}$=2+$\sqrt{3}$.
点评 此题主要考查了二次根式的化简,正确应用完全平方公式是解题关键.

练习册系列答案
相关题目
8.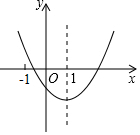 如图是二次函数y=ax2+bx+c的图象,其对称轴为直线x=1,则下列结论错误的是( )
如图是二次函数y=ax2+bx+c的图象,其对称轴为直线x=1,则下列结论错误的是( )
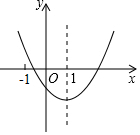 如图是二次函数y=ax2+bx+c的图象,其对称轴为直线x=1,则下列结论错误的是( )
如图是二次函数y=ax2+bx+c的图象,其对称轴为直线x=1,则下列结论错误的是( )| A. | a>0 | |
| B. | 2a+b=0 | |
| C. | a-b+c<0 | |
| D. | 若($\frac{1}{2}$,y1),(3,y2)是抛物线上两点,则y1<y2 |
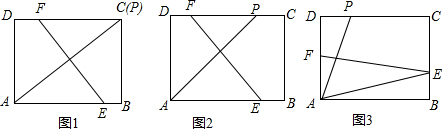
 如图,已知:$\frac{AD}{AB}$=$\frac{DE}{BC}$=$\frac{AE}{AC}$,求证:∠CAE=∠BAD.
如图,已知:$\frac{AD}{AB}$=$\frac{DE}{BC}$=$\frac{AE}{AC}$,求证:∠CAE=∠BAD.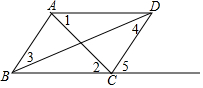 如图,
如图,