题目内容
8.有两条直线l1:y=ax+b和l2:y=cx-5,学生甲解出它们的交点为(2,-1);学生乙因把c抄错而解出它们的交点为(3,0),试求(a+b+c)2的值0.分析 把交点坐标和解错的坐标分别代入两直线y1=ax+b,y2=cx-5,解方程组即可求出.
解答 解:由题意可得$\left\{\begin{array}{l}{2a+b=-1}\\{3a+b=0}\\{2c-5=-1}\end{array}\right.$,
解得$\left\{\begin{array}{l}{a=1}\\{b=-3}\\{c=2}\end{array}\right.$,
故(a+b+c)2=0,
故答案为:0
点评 本题要注意利用一次函数的特点,列出方程组,求出未知数即可.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
18.已知a、b是方程x2-6x+8=0的两根,以a、b为边的等腰三角形的周长是( )
| A. | 10 | B. | 8或10 | C. | 8 | D. | 不确定 |
16.下列说法正确的是( )
| A. | 4的算术平方根是2 | B. | -8的立方根不存在 | ||
| C. | 1的平方根是1 | D. | -4的平方根是±2 |
3.函数y=a(x-a)(a<0)的图象不经过( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
 如图,正方形网格中每个小正方形的边长都是1,△ABC的三个顶点A、B、C都是格点(每个小正方形的顶点叫做格点).
如图,正方形网格中每个小正方形的边长都是1,△ABC的三个顶点A、B、C都是格点(每个小正方形的顶点叫做格点).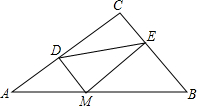 如图,在Rt△ABC中,∠C=90°,BC=3,AC=4,M为斜边AB上一动点,过M作MD⊥AC,过M作ME⊥CB于点E,则线段DE的最小值为$\frac{12}{5}$.
如图,在Rt△ABC中,∠C=90°,BC=3,AC=4,M为斜边AB上一动点,过M作MD⊥AC,过M作ME⊥CB于点E,则线段DE的最小值为$\frac{12}{5}$.