题目内容
18.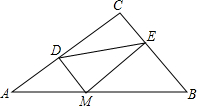 如图,在Rt△ABC中,∠C=90°,BC=3,AC=4,M为斜边AB上一动点,过M作MD⊥AC,过M作ME⊥CB于点E,则线段DE的最小值为$\frac{12}{5}$.
如图,在Rt△ABC中,∠C=90°,BC=3,AC=4,M为斜边AB上一动点,过M作MD⊥AC,过M作ME⊥CB于点E,则线段DE的最小值为$\frac{12}{5}$.
分析 连接CM,先证明四边形CDME是矩形,得出DE=CM,再由三角形的面积关系求出CM的最小值,即可得出结果.
解答 解:连接CM,如图所示: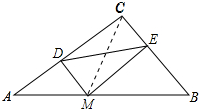
∵MD⊥AC,ME⊥CB,
∴∠MDC=∠MEC=90°,
∵∠C=90°,
∴四边形CDME是矩形,
∴DE=CM,
∵∠C=90°,BC=3,AC=4,
∴AB=$\sqrt{B{C}^{2}+A{C}^{2}}$=$\sqrt{{3}^{2}+{4}^{2}}$=5,
当CM⊥AB时,CM最短,此时△ABC的面积=$\frac{1}{2}$AB•CM=$\frac{1}{2}$BC•AC,
∴CM的最小值=$\frac{BC•AC}{AB}$=$\frac{12}{5}$,
∴线段DE的最小值为$\frac{12}{5}$;
故答案为:$\frac{12}{5}$.
点评 本题考查了矩形的判定与性质、勾股定理、直角三角形面积的计算方法;熟练掌握矩形的判定与性质,并能进行推理论证与计算是解决问题的关键.

练习册系列答案
 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案
相关题目
6. 如图所示,∠B=∠D=90°,BC=CD,∠1=40°,则∠2=( )
如图所示,∠B=∠D=90°,BC=CD,∠1=40°,则∠2=( )
 如图所示,∠B=∠D=90°,BC=CD,∠1=40°,则∠2=( )
如图所示,∠B=∠D=90°,BC=CD,∠1=40°,则∠2=( )| A. | 40° | B. | 50° | C. | 45° | D. | 60° |
10.下列说法中正确的是( )
| A. | 画一条3厘米长的直线 | B. | 画一条3厘米长的射线 | ||
| C. | 画一条3厘米长的线段 | D. | 在直线、射线、线段中直线最长 |
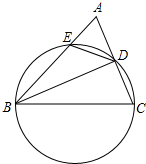 如图,在△ABC中,以BC为直径的圆分别交边AC、AB于D、E两点,连接BD、DE.若BD平分∠ABC.求证:
如图,在△ABC中,以BC为直径的圆分别交边AC、AB于D、E两点,连接BD、DE.若BD平分∠ABC.求证: 如图,线段AB的两个端点坐标分别为A(1,1),B(2,1),以原点O为位似中心,将线段AB放大后得到线段CD,若CD=2,则端点C的坐标为(2,2).
如图,线段AB的两个端点坐标分别为A(1,1),B(2,1),以原点O为位似中心,将线段AB放大后得到线段CD,若CD=2,则端点C的坐标为(2,2).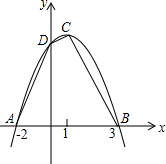 已知:如图,二次函数的图象与x轴交于A(-2,0),B(4,0)两点,且函数的最大值为9.
已知:如图,二次函数的图象与x轴交于A(-2,0),B(4,0)两点,且函数的最大值为9. 如图,在△ABC中,E,F是边BC上的两个三等分点,D是AC的中点,BD分别交AE,AF,AC于P,Q,D,求BP:PQ:QD.
如图,在△ABC中,E,F是边BC上的两个三等分点,D是AC的中点,BD分别交AE,AF,AC于P,Q,D,求BP:PQ:QD. 如图,在△ABC中,AC=4,AB=5,BC=6,点D、E分别在AB、AC上,且∠AED=∠B,如果四边形BCED的周长为13,求DE的长.
如图,在△ABC中,AC=4,AB=5,BC=6,点D、E分别在AB、AC上,且∠AED=∠B,如果四边形BCED的周长为13,求DE的长.