题目内容
18.已知a、b是方程x2-6x+8=0的两根,以a、b为边的等腰三角形的周长是( )| A. | 10 | B. | 8或10 | C. | 8 | D. | 不确定 |
分析 求出方程的解x1=2,x2=4,分为两种情况:①当等腰三角形的三边是2、2、4时,此时不符合三角形的三边关系定理,舍去;②当等腰三角形的三边是2、4、4时,此时符合三角形的三边关系定理,求出答案即可.
解答 解:∵方程x2-6x+8=0的两根分别为x1=2,x2=4,
又∵a、b是方程x2-6x+8=0的两根,且a、b为等腰三角形的边长,
∴a=2为等腰三角形的腰长,那么等腰三角形的底边长为4,
又∵2+2=4,
∴边长分别为2,2,4不能构成三角形,故舍去,
∴此等腰三角形的腰长为4,底边长为2,
∴此等腰三角形的周长=4+4+2=10.
故选:A.
点评 本题考查了等腰三角形性质,解一元二次方程,三角形的三边关系定理的应用,解答本题关键是能求出符合条件的所有情况,此题难度不大.

练习册系列答案
 优生乐园系列答案
优生乐园系列答案 新编小学单元自测题系列答案
新编小学单元自测题系列答案
相关题目
6. 不等式的解集在数轴上表示如图所示,则这个不等式为( )
不等式的解集在数轴上表示如图所示,则这个不等式为( )
 不等式的解集在数轴上表示如图所示,则这个不等式为( )
不等式的解集在数轴上表示如图所示,则这个不等式为( )| A. | x+2>0 | B. | x+2<0 | C. | x≥-2 | D. | x≤-2 |
13.下列各式中,运算正确的是( )
| A. | 2x2-x=x2 | B. | (x2)3=x5 | C. | 2$\sqrt{3}+3\sqrt{3}=5\sqrt{3}$ | D. | x2•x3=x6 |
10.在平面直角坐标系中,反比例函数y=$\frac{{a}^{2}-a+1}{x}$图象的两个分支分别在( )
| A. | 第一、二象限 | B. | 第三、四象限 | C. | 第二、四象限 | D. | 第一、三象限 |
7.若⊙O的半径为4cm,点A到圆心O的距离为4.5cm,那么点A与⊙O的位置关系是( )
| A. | 点A在圆内 | B. | 点A在圆上 | C. | 点A在圆外 | D. | 不能确定 |
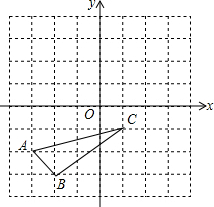 如图,△ABC是格点三角形,且A(-3,-2),B(-2,-3),C(1,-1)
如图,△ABC是格点三角形,且A(-3,-2),B(-2,-3),C(1,-1)