题目内容
18.设关于x的方程2x2-mx-m2-2=0有整数根,求整数m.分析 由2x2-mx-m2-2=0,得到2x2-mx-m2=2,由于x,m均为整数,得到$\left\{\begin{array}{l}{2x+m=2}\\{x-m=1}\end{array}\right.$或$\left\{\begin{array}{l}{2x+m=-2}\\{x-m=-1}\end{array}\right.$,即可得到结论.
解答 解:∵2x2-mx-m2-2=0,
∴2x2-mx-m2=2,
∵x,m均为整数,
∴$\left\{\begin{array}{l}{2x+m=2}\\{x-m=1}\end{array}\right.$或$\left\{\begin{array}{l}{2x+m=-2}\\{x-m=-1}\end{array}\right.$,
若x-m=2,则x,m为偶数,
∴2x+m为偶数与2x+m=1矛盾,
∴不成立,
解得:$\left\{\begin{array}{l}{x=1}\\{m=0}\end{array}\right.$,$\left\{\begin{array}{l}{x=-1}\\{m=0}\end{array}\right.$,
∴m=0.
点评 此题考查了根的判别式,根的判别式大于0,方程有两个不相等的实数根;根的判别式等于0,方程有两个相等的实数根;根的判别式小于0,方程没有实数根.以及根与系数的关系.

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目
 如图,EP∥AB,PF∥CD,∠B=100°,∠C=120°,求∠EPF的度数.
如图,EP∥AB,PF∥CD,∠B=100°,∠C=120°,求∠EPF的度数.
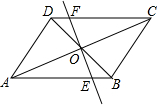 如图,在?ABCD中,对角线AC与BD相交于点O,∠ADB=90°,过O作EF⊥AC交AB于E,交CD于F.
如图,在?ABCD中,对角线AC与BD相交于点O,∠ADB=90°,过O作EF⊥AC交AB于E,交CD于F.
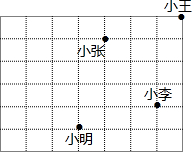 建立适当的直角坐标系,使得小明坐标为(3,-1),写出小张、小王、小李的坐标:
建立适当的直角坐标系,使得小明坐标为(3,-1),写出小张、小王、小李的坐标: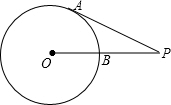 如图,已知PA切⊙O于点A,PO交⊙O于点B,若PA=6,BP=4,则⊙O的半径为2.5.
如图,已知PA切⊙O于点A,PO交⊙O于点B,若PA=6,BP=4,则⊙O的半径为2.5.