题目内容
5．
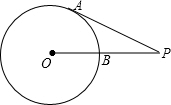如图，已知PA切⊙O于点A，PO交⊙O于点B，若PA=6，BP=4，则⊙O的半径为2.5．
分析 连接OA，由切线的性质可证△AOP为直角三角形，再利用勾股定理求半径OA．
解答 解：连接OA．
∵PA切⊙O于A点，
∴OA⊥AP，
在Rt△AOP中，设OA=OB=r，
则OA2+AP2=OP2，即r2+62=（r+4）2，
解得r=2.5，
即⊙O的半径为2.5，
故答案为：2.5．
点评 本题考查了切线的性质，勾股定理的运用．关键是由切线的性质构造直角三角形，运用勾股定理列方程求解．
练习册系列答案
相关题目
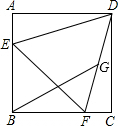如图，边长为4的正三角形DEF与正方形ABCD共有一顶点D，点E、F分别在线段AB、BC上，将点B与线段DF的中点G连接，则线段BG的长是$\sqrt{6}$+$\sqrt{2}$．
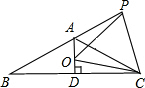如图，在等腰△ABC中，AB=AC，∠BAC=120°，AD⊥BC于点D，点P是BA延长线上一点，点O是线段AD上一点，OP=OC，若BC=2$\sqrt{3}$，AD=1，则S四边形AOCP=$\sqrt{3}$．