题目内容
3.已知抛物线y=x2+bx+9经过点(1,2).(1)求抛物线的解析式及顶点坐标;
(2)若点(x1,y1)和点(x2,y2)均在抛物线上,且x1<x2,要使y1>y2,则求x1与x2满足的条件.
分析 (1)用待定系数法即可求出抛物线的解析式,再利用配方法求出顶点坐标.
(2)利用图象分两种情形讨论①x1、x2都在对称轴左侧面,②x1在对称轴左边,x2在对称右边.列出不等式可以解决.
解答 解:(1)∵抛物线y=x2+bx+9经过点(1,2),
∴2=1+b+9,
∴b=-8,
∴抛物线解析式为y=x2-8x+9,
∵y=x2-8x+9=(x-4)2-7,
∴顶点坐标为(4,-7)
(2)由图象可知:①x1<x2<4时,y1>y2,②x2-4<4-x1,即x1+x2<8时,y1>y2,
综上所述:x1+x2<8时,y1>y2.
点评 本题考查二次函数与不等式、待定系数法确定二次函数的解析式,掌握配方法求顶点坐标,学会根据图象说出函数的增减性,属于中考常考题型.

练习册系列答案
 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案
相关题目
14.已知点M(x,-1)与N(2,y)关于y轴对称,则xy的值为( )
| A. | -2 | B. | 2 | C. | -1 | D. | 4 |
15.已知点A(-1,m)和B(1,n)在函数y=$\frac{1}{3}$x+k的图象上,则下列结论中一定正确的是( )
| A. | m>n | B. | m<n | C. | k>0 | D. | k<0 |
 如图,在?ABCD中,AB=4,BC=8,∠B=60°,点P以每秒2个单位速度,从点B出发沿射线BA方向运动,同时直线l以每秒1个单位速度,从CD出发沿射线CB方向运动,分别交BC,AC于点G,H,连结PG,设运动的时间为t,当G与B重合时,运动停止.
如图,在?ABCD中,AB=4,BC=8,∠B=60°,点P以每秒2个单位速度,从点B出发沿射线BA方向运动,同时直线l以每秒1个单位速度,从CD出发沿射线CB方向运动,分别交BC,AC于点G,H,连结PG,设运动的时间为t,当G与B重合时,运动停止.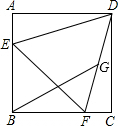 如图,边长为4的正三角形DEF与正方形ABCD共有一顶点D,点E、F分别在线段AB、BC上,将点B与线段DF的中点G连接,则线段BG的长是$\sqrt{6}$+$\sqrt{2}$.
如图,边长为4的正三角形DEF与正方形ABCD共有一顶点D,点E、F分别在线段AB、BC上,将点B与线段DF的中点G连接,则线段BG的长是$\sqrt{6}$+$\sqrt{2}$.