题目内容
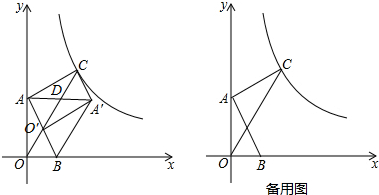
9.已知,在平面直角从标系中,A点坐标为(0,4),B点坐标为(2,0),C(m,6)为反比例函数$y=\frac{{12\sqrt{3}}}{x}$图象上一点.将△AOB绕B点旋转至△A′O′B处.(1)求m的值;
(2)若O′落在OC上,连接AA′交OC与D点.①求证:四边形ACA′O′为平行四边形; ②求CD的长度;
(3)直接写出当AO′最短和最长时A′点的坐标.
分析 (1)只需把点C的坐标代入反比例函数的解析式,就可解决问题;
(2)①过点C作CH⊥y轴与H,如图1,易证AC=OA=O′A′,要证四边形ACA′O′为平行四边形,只需证AC∥O′A′,只需证∠ACO=∠A′O′C即可;
②由平行四边形ACA′O′可得CD=$\frac{1}{2}$CO′,要求CD,只需求CO′,只需求出OC及OO′即可;
(3)根据两点之间线段最短可知:当点O′在线段AB上时AO′最短(如图2),当点O′在线段AB的延长线上时AO′最长(如图3);过点O′作O′N⊥x轴于N,过点A′作A′M⊥O′N于M,易证△BNO′∽△BOA,△A′MO′∽△O′NB,然后只需运用相似三角形的性质即可解决问题.
解答 解:(1)∵C(m,6)为反比例函数$y=\frac{{12\sqrt{3}}}{x}$图象上一点,
∴m=$\frac{12\sqrt{3}}{6}$=2$\sqrt{3}$;
(2)①过点C作CH⊥y轴与H,如图1.
∵点C的坐标为(2$\sqrt{3}$,6),
∴CH=2$\sqrt{3}$,OH=6,
∴tan∠COH=$\frac{2\sqrt{3}}{6}$=$\frac{\sqrt{3}}{3}$,AC=$\sqrt{(6-4)^{2}+(2\sqrt{3})^{2}}$=4,
∴∠COH=30°,OA=AC,
∴∠BOO′=60°,∠ACO=∠AOC=30°.
∵BO′=BO,
∴∠BO′O=∠BOO′=60°.
∵∠A′O′B=∠AOB=90°,
∴∠CO′A′=30°,
∴∠ACO=∠CO′A′,
∴AC∥O′A′.
又∵O′A′=OA=AC,
∴四边形ACA′O′为平行四边形;
②∵BO′=BO,∠BOO′=60°,
∴△BOB′是等边三角形,
∴OO′=OB=2.
∵∠CHO=90°,CH=2$\sqrt{3}$,OH=6,
∴OC=4$\sqrt{3}$,
∴CO′=OC-OO′=4$\sqrt{3}$-2.
∵四边形ACA′O′为平行四边形,
∴CD=O′D=$\frac{1}{2}$CO′=2$\sqrt{3}$-1;
(3)当AO′最短时A′点的坐标(2+$\frac{6\sqrt{5}}{5}$,$\frac{8\sqrt{5}}{5}$),当AO′最长时A′点的坐标(2-$\frac{6\sqrt{5}}{5}$,-$\frac{8\sqrt{5}}{5}$).
提示:①当点O′在线段AB上时,AO′最短,
过点O′作O′N⊥x轴于N,过点A′作A′M⊥O′N于M,如图2.
∵O′N∥OA,
∴△BNO′∽△BOA,
∴$\frac{BN}{BO}$=$\frac{O′N}{OA}$=$\frac{BO′}{BA}$,
∴$\frac{BN}{2}$=$\frac{O′N}{4}$=$\frac{2}{2\sqrt{5}}$,
∴BN=$\frac{2\sqrt{5}}{5}$,O′N=$\frac{4\sqrt{5}}{5}$.
∵∠A′MO′=∠A′O′B=∠O′NB=90°,
∴∠MA′O′=∠NO′B,
∴△A′MO′∽△O′NB,
∴$\frac{A′M}{O′N}=\frac{O′M}{BN}=\frac{O′A′}{O′B}$=$\frac{4}{2}$=2,
∴A′M=$\frac{8\sqrt{5}}{5}$,O′M=$\frac{4\sqrt{5}}{5}$,
∴A′(2-$\frac{2\sqrt{5}}{5}$+$\frac{8\sqrt{5}}{5}$,$\frac{4\sqrt{5}}{5}$+$\frac{4\sqrt{5}}{5}$)即(2+$\frac{6\sqrt{5}}{5}$,$\frac{8\sqrt{5}}{5}$);
②当点O′在线段AB延长线上时,AO′最长,
过点O′作O′N⊥x轴于N,过点A′作A′M⊥O′N于M,如图3.
同理可得:A′(2-$\frac{6\sqrt{5}}{5}$,-$\frac{8\sqrt{5}}{5}$).
点评 本题主要考查了反比例函数图象上点的坐标特征、旋转的性质、相似三角形的判定与性质、平行四边形的判定与性质、等边三角形的判定与性质、三角函数的定义、特殊角的三角函数值、勾股定理等知识,利用平行四边形的对角线互相平分是解决第(2)②小题的关键,构造K型相似是解决第(3)小题的关键.

 教材全解字词句篇系列答案
教材全解字词句篇系列答案| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | $\frac{1}{3}$ | D. | 1 |
| A. | (a+6)(a-6)=a2-36 | B. | x2-8x+16=(x-4)2 | ||
| C. | a2-b2+1=(a+b)(a-b)+1 | D. | (x-2)(x+3)=(x+3)(x-2) |
| A. | -2 | B. | 2 | C. | -1 | D. | 4 |
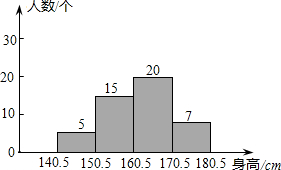 某校测量了初三(1)班学生的身高(精确到1cm),按10cm为一段进行分组,得到如图频数分布直方图,则下列说法正确的是( )
某校测量了初三(1)班学生的身高(精确到1cm),按10cm为一段进行分组,得到如图频数分布直方图,则下列说法正确的是( )| A. | 该班人数最多的身高段的学生数为7人 | |
| B. | 该班身高最高段的学生数为7人 | |
| C. | 该班身高最高段的学生数为20人 | |
| D. | 该班身高低于160.5cm的学生数为15人 |
