题目内容
3.观察下列各式:①$\sqrt{2+\frac{2}{3}}=2\sqrt{\frac{2}{3}}$;②$\sqrt{3+\frac{3}{8}}=3\sqrt{\frac{3}{8}}$;③$\sqrt{4+\frac{4}{15}}=4\sqrt{\frac{4}{15}}$.(1)上面各式成立吗?请写出验证过程;
(2)请用字母n(n是正整数且n≥2)表示上面三个式子的规律,并给出证明.
分析 (1)利用二次根式的化简进行验证即可;
(2)根据等式的左右两边的变化规律可写出其式子的规律,利用二次根式的化简可证明.
解答 解:
(1)成立.
验证如下:
①$\sqrt{2+\frac{2}{3}}$=$\sqrt{\frac{6+2}{3}}$=$\sqrt{\frac{8}{3}}$=$\sqrt{\frac{4×2}{3}}$=2$\sqrt{\frac{2}{3}}$,
②$\sqrt{3+\frac{3}{8}}$=$\sqrt{\frac{24+3}{8}}$=$\sqrt{\frac{27}{8}}$=$\sqrt{\frac{9×3}{8}}$=3$\sqrt{\frac{3}{8}}$,
③$\sqrt{4+\frac{4}{15}}$=$\sqrt{\frac{60+4}{15}}$=$\sqrt{\frac{64}{15}}$=$\sqrt{\frac{16×4}{15}}$=4$\sqrt{\frac{4}{15}}$,
∴各式都成立;
(2)规律:$\sqrt{n+\frac{n}{{n}^{2}-1}}$=n$\sqrt{\frac{n}{{n}^{2}-1}}$,
证明:
∵$\sqrt{n+\frac{n}{{n}^{2}-1}}$=$\sqrt{\frac{n({n}^{2}-1)+n}{{n}^{2}-1}}$=$\sqrt{\frac{{n}^{3}}{{n}^{2}-1}}$=$\sqrt{\frac{{n}^{2}•n}{{n}^{2}-1}}$=n$\sqrt{\frac{n}{{n}^{2}-1}}$,
∴等式成立.
点评 本题主要考查二次根式的化简,掌握二次根式的性质是解题的关键,即$\sqrt{{a}^{2}}$=|a|.

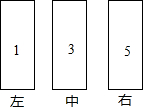 如图,敲击三根管时依次发出“1”、“3”“5”,两只音锤同时从“1”开始,以相同的节拍往复敲击,不同的是:甲锤每拍移动一位(左中右中左中右…),乙锤则在两端各有一拍不移位(左中右右中左左中右…),在第200拍时,你听到的是( )
如图,敲击三根管时依次发出“1”、“3”“5”,两只音锤同时从“1”开始,以相同的节拍往复敲击,不同的是:甲锤每拍移动一位(左中右中左中右…),乙锤则在两端各有一拍不移位(左中右右中左左中右…),在第200拍时,你听到的是( )| A. | 同样的音“1” | B. | 同样的音“3” | C. | 同样的音“5” | D. | 不同的两个音 |
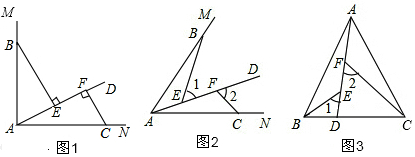
 如图,CE是△ABC的外角∠ACD的平分线,若∠B=35°,∠ACE=60°,则∠A=85°.
如图,CE是△ABC的外角∠ACD的平分线,若∠B=35°,∠ACE=60°,则∠A=85°.