题目内容
4.已知a+b=5,ab=3,求a2+b2的值.解法展示:∵a+b=5,∴(a+b)2=52.
∴a2+2ab+b2=25.
∵ab=3,∴a2+6+b2=25.∴a2+b2=19.
合作交流:(1)上述解法主要用了哪些我们学过的公式和法则?请写出一条.
(2)若x满足(210-x)(x-200)=-204,试求(210-x)2+(x-200)2的值.
(3)已x+$\frac{1}{x}$=-2,求x2+$\frac{1}{{x}^{2}}$和x4+$\frac{1}{{x}^{4}}$的值.
分析 (1)根据例题中用了完全平方公式即可解答;
(2)利用完全平方公式,则[(210-x)+(x-200)]2=(210-x)2+(x-200)2+2(210-x)(x-200),据此即可求解;
(3)x+$\frac{1}{x}$=-2两边平方即可求得x2+$\frac{1}{{x}^{2}}$,然后对这个式子平方即可求得x4+$\frac{1}{{x}^{4}}$.
解答 解:(1)利用的完全平方公式;
(2)∵[(210-x)+(x-200)]2=(210-x)2+(x-200)2+2(210-x)(x-200)=100,
∴(210-x)2+(x-200)2=100-2(210-x)(x-200)=100+2×204=508;
(3)x+$\frac{1}{x}$=-2两边平方得:x2+2+$\frac{1}{{x}^{2}}$=4,
则x2+$\frac{1}{{x}^{2}}$=2;
两边平方得x4+2+$\frac{1}{{x}^{4}}$=4,
则x4+$\frac{1}{{x}^{4}}$=2.
点评 本题考查了完全平方公式,注意公式的变形是解决本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
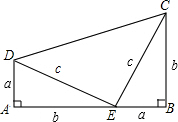 如图,这是美国第20届总统加菲尔德的构图,其中Rt△ADE和Rt△BEC是完全相同的,请你试用此图形验证勾股定理的正确性.
如图,这是美国第20届总统加菲尔德的构图,其中Rt△ADE和Rt△BEC是完全相同的,请你试用此图形验证勾股定理的正确性. 有理数a,b,c在数轴上的位置如图所示,化简|c-b|+|a-c|+|b-c|.
有理数a,b,c在数轴上的位置如图所示,化简|c-b|+|a-c|+|b-c|. 如图,在△ABC中,点D为边AB上一点,点F为BC延长线上一点,且AD=CF,连结DF,与AC相交于点E,点G为AC上一点,DG∥BC,△ADG∽△ABC,△EDG∽△EFC,那么$\frac{AB}{BC}$=$\frac{EF}{DE}$吗?为什么?
如图,在△ABC中,点D为边AB上一点,点F为BC延长线上一点,且AD=CF,连结DF,与AC相交于点E,点G为AC上一点,DG∥BC,△ADG∽△ABC,△EDG∽△EFC,那么$\frac{AB}{BC}$=$\frac{EF}{DE}$吗?为什么?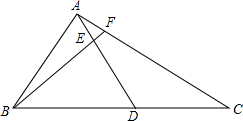 △ABC中,D为BC上的一点,$\frac{BD}{DC}=2$,E是AD上一点,$\frac{AE}{ED}=\frac{1}{4}$,求$\frac{BE}{EF}$,$\frac{AF}{FC}$的值.
△ABC中,D为BC上的一点,$\frac{BD}{DC}=2$,E是AD上一点,$\frac{AE}{ED}=\frac{1}{4}$,求$\frac{BE}{EF}$,$\frac{AF}{FC}$的值.