题目内容
14.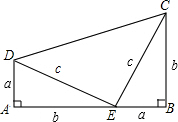 如图,这是美国第20届总统加菲尔德的构图,其中Rt△ADE和Rt△BEC是完全相同的,请你试用此图形验证勾股定理的正确性.
如图,这是美国第20届总统加菲尔德的构图,其中Rt△ADE和Rt△BEC是完全相同的,请你试用此图形验证勾股定理的正确性.
分析 此梯形的面积有三部分组成,利用梯形的面积等于三个直角三角形的面积之和列出方程并整理.
解答 证明:因为${S}_{梯形ABCD}=\frac{1}{2}•AB•(AD+BC)=\frac{1}{2}(a+b)(a+b)=\frac{1}{2}{a}^{2}+ab+\frac{1}{2}{b}^{2}$,
又因为${S}_{梯形ABCD}={S}_{△ADE}+{S}_{△DEC}+{S}_{△BEC}=\frac{1}{2}•AD•AE+\frac{1}{2}•DE•CE+\frac{1}{2}•BE•BC=\frac{1}{2}ab+\frac{1}{2}{c}^{2}+\frac{1}{2}ab=ab+\frac{1}{2}{c}^{2}$,所以$\frac{1}{2}{a}^{2}+ab+\frac{1}{2}{b}^{2}=ab+\frac{1}{2}{c}^{2}$,
得c2=a2+b2.
点评 此题考查勾股定理的证明,此类证明要转化成同一个东西的两种表示方法,从而转化成方程达到证明的结果.

练习册系列答案
 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案
相关题目
5.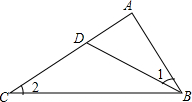 如图,下列条件:①∠1=∠2;②∠ADB=∠ABC;③AB2=AD•AC;④$\frac{AD}{AB}=\frac{BD}{BC}$,能使△ABD∽△ACB的条件的个数为( )
如图,下列条件:①∠1=∠2;②∠ADB=∠ABC;③AB2=AD•AC;④$\frac{AD}{AB}=\frac{BD}{BC}$,能使△ABD∽△ACB的条件的个数为( )
 如图,下列条件:①∠1=∠2;②∠ADB=∠ABC;③AB2=AD•AC;④$\frac{AD}{AB}=\frac{BD}{BC}$,能使△ABD∽△ACB的条件的个数为( )
如图,下列条件:①∠1=∠2;②∠ADB=∠ABC;③AB2=AD•AC;④$\frac{AD}{AB}=\frac{BD}{BC}$,能使△ABD∽△ACB的条件的个数为( )| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
9.如果等腰三角形两边长是10cm和5cm,那么它的周长是( )
| A. | 25cm | B. | 20cm | C. | 25cm或20cm | D. | 15cm |
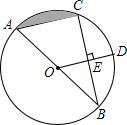 如图,AB是⊙O的直径,BC是⊙O的弦,半径OD⊥BC,垂足为E,若BC=2$\sqrt{3}$,DE=1,求:
如图,AB是⊙O的直径,BC是⊙O的弦,半径OD⊥BC,垂足为E,若BC=2$\sqrt{3}$,DE=1,求: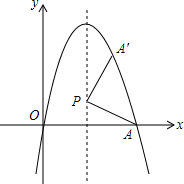 如图,经过原点的抛物线y=-x2+6x与x轴的另一个交点为A.
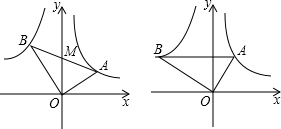
如图,经过原点的抛物线y=-x2+6x与x轴的另一个交点为A.