题目内容
15.已知m是实数,求|m|+|m-1|+|m-2|的最小值.分析 利用分类讨论当m≥2时,当1≤m≤2时,当0≤m≤1时,当m<0时,分别得出最小值进而得出答案.
解答 解:当m≥2时,|m|+|m-1|+|m-2|=m+m-1+m-2=3m-3=3(m-1)≥2;
当1≤m≤2时,|m|+|m-1|+|m-2|=m+m-1+2-m=m+1≥2;
当0≤m≤1时,|m|+|m-1|+|m-2|=m+1-m+2-m=-m+3≥2;
当m<0时,|m|+|m-1|+|m-2|=-m+1-m+2-m=-3m+3=-3(m-1)≥3;
综合所述:可得当m=1时可以得到它的最小值,最小值为2.
点评 此题主要考查了绝对值,利用m的取值范围不同分别分析求解是解题关键.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
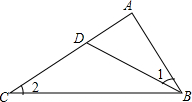 如图,下列条件:①∠1=∠2;②∠ADB=∠ABC;③AB2=AD•AC;④$\frac{AD}{AB}=\frac{BD}{BC}$,能使△ABD∽△ACB的条件的个数为( )
如图,下列条件:①∠1=∠2;②∠ADB=∠ABC;③AB2=AD•AC;④$\frac{AD}{AB}=\frac{BD}{BC}$,能使△ABD∽△ACB的条件的个数为( )
 如图,?ABCD中,点E在CD延长线上,连结BE交AD于点F,若AB=3,BC=4,DF=1,求DE的长.
如图,?ABCD中,点E在CD延长线上,连结BE交AD于点F,若AB=3,BC=4,DF=1,求DE的长.