题目内容
数学问题：计算
+
+
+…+
（其中m，n都是正整数，且m≥2，n≥1）．
探究问题：为解决上面的数学问题，我们运用数形结合的思想方法，通过不断地分割一个面积为1的正方形，把数量关系和几何图形巧妙地结合起来，并采取一般问题特殊化的策略来进行探究．
探究一：计算
+
+
+…+
．
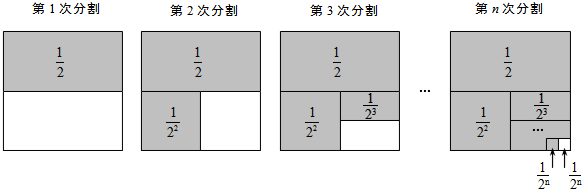
第1次分割，把正方形的面积二等分，其中阴影部分的面积为
；
第2次分割，把上次分割图中空白部分的面积继续二等分，阴影部分的面积之和为
+
；
第3次分割，把上次分割图中空白部分的面积继续二等分，…；
…
第n次分割，把上次分割图中空白部分的面积最后二等分，所有阴影部分的面积之和为
+
+
+…+
，最后空白部分的面积是
．
根据第n次分割图可得等式：
+
+
+…+
=1-
．
探究二：计算
+
+
+…+
．
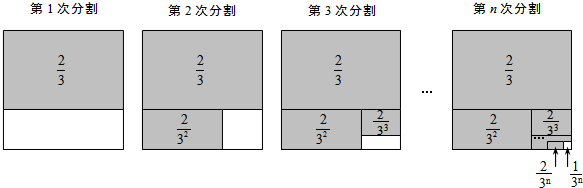
第1次分割，把正方形的面积三等分，其中阴影部分的面积为
；
第2次分割，把上次分割图中空白部分的面积继续三等分，阴影部分的面积之和为
+
；
第3次分割，把上次分割图中空白部分的面积继续三等分，…；
…
第n次分割，把上次分割图中空白部分的面积最后三等分，所有阴影部分的面积之和为
+
+
+…+
，最后空白部分的面积是
．
根据第n次分割图可得等式：
+
+
+…+
=1-
，
两边同除以2，得
+
+
+…+
=
-
．
探究三：计算
+
+
+…+
．
（仿照上述方法，只画出第n次分割图，在图上标注阴影部分面积，并写出探究过程）
解决问题：计算
+
+
+…+
．
（只需画出第n次分割图，在图上标注阴影部分面积，并完成以下填空）
根据第n次分割图可得等式： ，
所以，
+
+
+…+
= ．
拓广应用：计算
+
+
+…+
．
| 1 |
| m |
| 1 |
| m2 |
| 1 |
| m3 |
| 1 |
| mn |
探究问题：为解决上面的数学问题，我们运用数形结合的思想方法，通过不断地分割一个面积为1的正方形，把数量关系和几何图形巧妙地结合起来，并采取一般问题特殊化的策略来进行探究．
探究一：计算
| 1 |
| 2 |
| 1 |
| 22 |
| 1 |
| 23 |
| 1 |
| 2n |
第1次分割，把正方形的面积二等分，其中阴影部分的面积为
| 1 |
| 2 |
第2次分割，把上次分割图中空白部分的面积继续二等分，阴影部分的面积之和为
| 1 |
| 2 |
| 1 |
| 22 |
第3次分割，把上次分割图中空白部分的面积继续二等分，…；
…
第n次分割，把上次分割图中空白部分的面积最后二等分，所有阴影部分的面积之和为
| 1 |
| 2 |
| 1 |
| 22 |
| 1 |
| 23 |
| 1 |
| 2n |
| 1 |
| 2n |
根据第n次分割图可得等式：
| 1 |
| 2 |
| 1 |
| 22 |
| 1 |
| 23 |
| 1 |
| 2n |
| 1 |
| 2n |
探究二：计算
| 1 |
| 3 |
| 1 |
| 32 |
| 1 |
| 33 |
| 1 |
| 3n |
第1次分割，把正方形的面积三等分，其中阴影部分的面积为
| 2 |
| 3 |
第2次分割，把上次分割图中空白部分的面积继续三等分，阴影部分的面积之和为
| 2 |
| 3 |
| 2 |
| 32 |
第3次分割，把上次分割图中空白部分的面积继续三等分，…；
…
第n次分割，把上次分割图中空白部分的面积最后三等分，所有阴影部分的面积之和为
| 2 |
| 3 |
| 2 |
| 32 |
| 2 |
| 33 |
| 2 |
| 3n |
| 1 |
| 3n |
根据第n次分割图可得等式：
| 2 |
| 3 |
| 2 |
| 32 |
| 2 |
| 33 |
| 2 |
| 3n |
| 1 |
| 3n |
两边同除以2，得
| 1 |
| 3 |
| 1 |
| 32 |
| 1 |
| 33 |
| 1 |
| 3n |
| 1 |
| 2 |
| 1 |
| 2×3n |
探究三：计算
| 1 |
| 4 |
| 1 |
| 42 |
| 1 |
| 43 |
| 1 |
| 4n |
（仿照上述方法，只画出第n次分割图，在图上标注阴影部分面积，并写出探究过程）
解决问题：计算
| 1 |
| m |
| 1 |
| m2 |
| 1 |
| m3 |
| 1 |
| mn |
（只需画出第n次分割图，在图上标注阴影部分面积，并完成以下填空）
根据第n次分割图可得等式：
所以，
| 1 |
| m |
| 1 |
| m2 |
| 1 |
| m3 |
| 1 |
| mn |
拓广应用：计算
| 5-1 |
| 5 |
| 52-1 |
| 52 |
| 53-1 |
| 53 |
| 5n-1 |
| 5n |
考点：作图—应用与设计作图,规律型：图形的变化类
专题：压轴题,阅读型,规律型
分析：探究三：根据探究二的分割方法依次进行分割，然后表示出阴影部分的面积，再除以3即可；
解决问题：按照探究二的分割方法依次分割，然后表示出阴影部分的面积及，再除以（m-1）即可得解；
拓广应用：先把每一个分数分成1减去一个分数，然后应用公式进行计算即可得解．
解决问题：按照探究二的分割方法依次分割，然后表示出阴影部分的面积及，再除以（m-1）即可得解；
拓广应用：先把每一个分数分成1减去一个分数，然后应用公式进行计算即可得解．
解答：解：探究三：第1次分割，把正方形的面积四等分，
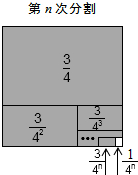
其中阴影部分的面积为
；
第2次分割，把上次分割图中空白部分的面积继续四等分，
阴影部分的面积之和为
+
；
第3次分割，把上次分割图中空白部分的面积继续四等分，
…，
第n次分割，把上次分割图中空白部分的面积最后四等分，
所有阴影部分的面积之和为：
+
+
+…+
，
最后的空白部分的面积是
，
根据第n次分割图可得等式：
+
+
+…+
=1-
，
两边同除以3，得
+
+
+…+
=
-
；
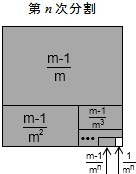
解决问题：
+
+
+…+
=1-
，
+
+
+…+
=
-
；
故答案为：
+
+
+…+
=1-
，
-
；
拓广应用：
+
+
+…+
，
=1-
+1-
+1-
+…+1-
，
=n-（
+
+
+…+
），
=n-（
-
），
=n-
+
．
其中阴影部分的面积为
| 3 |
| 4 |
第2次分割，把上次分割图中空白部分的面积继续四等分，
阴影部分的面积之和为
| 3 |
| 4 |
| 3 |
| 42 |
第3次分割，把上次分割图中空白部分的面积继续四等分，
…，
第n次分割，把上次分割图中空白部分的面积最后四等分，
所有阴影部分的面积之和为：
| 3 |
| 4 |
| 3 |
| 42 |
| 3 |
| 43 |
| 3 |
| 4n |
最后的空白部分的面积是
| 1 |
| 4n |
根据第n次分割图可得等式：
| 3 |
| 4 |
| 3 |
| 42 |
| 3 |
| 43 |
| 3 |
| 4n |
| 1 |
| 4n |
两边同除以3，得
| 1 |
| 4 |
| 1 |
| 42 |
| 1 |
| 43 |
| 1 |
| 4n |
| 1 |
| 3 |
| 1 |
| 3×42 |
解决问题：
| m-1 |
| m |
| m-1 |
| m2 |
| m-1 |
| m3 |
| m-1 |
| mn |
| 1 |
| mn |
| 1 |
| m |
| 1 |
| m2 |
| 1 |
| m3 |
| 1 |
| mn |
| 1 |
| m-1 |
| 1 |
| (m-1)×mn |
故答案为：
| 3 |
| 4 |
| 3 |
| 42 |
| 3 |
| 43 |
| 3 |
| 4n |
| 1 |
| 4n |
| 1 |
| m-1 |
| 1 |
| (m-1)×mn |
拓广应用：
| 5-1 |
| 5 |
| 52-1 |
| 52 |
| 53-1 |
| 53 |
| 5n-1 |
| 5n |
=1-
| 1 |
| 5 |
| 1 |
| 52 |
| 1 |
| 53 |
| 1 |
| 5n |
=n-（
| 1 |
| 5 |
| 1 |
| 52 |
| 1 |
| 53 |
| 1 |
| 5n |
=n-（
| 1 |
| 4 |
| 1 |
| 4×5n |
=n-
| 1 |
| 4 |
| 1 |
| 4×5n |
点评：本题考查了应用与设计作图，图形的变化规律，读懂题目信息，理解分割的方法以及求和的方法是解题的关键．
练习册系列答案
相关题目
如图：一个残破的圆钢轮，为了再铸做一个同样大小的圆轮，请用圆规、直尺作出它的圆心（不用写作法，保留作图痕迹）．
如图，在△ABC中，AB=AC，D为BC中点，四边形ABDE是平行四边形．
马航MH370航班于2014年3月8日凌晨与地面失去了联系，至今尚未找到有关马航MH370的任何消息．我国在第一时间派出了飞机和船只进行寻找．如图，某日在马航MH370失联的附近海域有两艘自西向东航行的海监船A、B正在执行搜索任务，B船在A船的正东方向，且两船保持20海里的距离，某一时刻在海监船A的东北方向，B的北偏东15°方向的我国渔政执法船C侦测到了疑似物品，上级命令B船马上前去支援，已知B船的速度是30海里/小时，求B船到达C船的时间是多少．（结果保留根号）
如图，若AB是⊙O的直径，CD是⊙O的弦，∠ABD=60°，则∠BCD=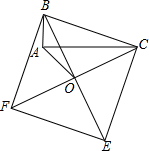
如图，以Rt△ABC的斜边BC为一边在△ABC的同侧作正方形BCEF，设正方形的中心为O，连结A0．如果AB=3，AO=2，那么AC的长等于