题目内容
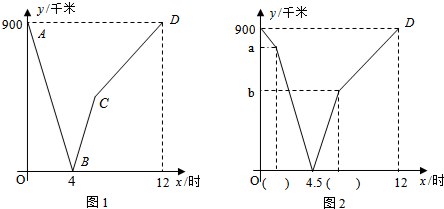
 如图,以Rt△ABC的斜边BC为一边在△ABC的同侧作正方形BCEF,设正方形的中心为O,连结A0.如果AB=3,AO=2,那么AC的长等于
如图,以Rt△ABC的斜边BC为一边在△ABC的同侧作正方形BCEF,设正方形的中心为O,连结A0.如果AB=3,AO=2,那么AC的长等于考点:全等三角形的判定与性质,等腰直角三角形,正方形的性质
专题:
分析:在AC上截取CG=AB=3,连接OG,根据B、A、O、C四点共圆,推出∠ABO=∠ACO,证△BAO≌△CGO,推出OA=OG=2,∠AOB=∠COG,得出等腰直角三角形AOG,根据勾股定理求出AG,即可求出AC.
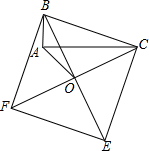
解答: 解:在AC上截取CG=AB=3,连接OG,
解:在AC上截取CG=AB=3,连接OG,
∵四边形BCEF是正方形,∠BAC=90°,
∴OB=OC,∠BAC=∠BOC=90°,
∴B、A、O、C四点共圆,
∴∠ABO=∠ACO,
在△BAO和△CGO中
,
∴△BAO≌△CGO(SAS),
∴OA=OG=2,∠AOB=∠COG,
∵∠BOC=∠COG+∠BOG=90°,
∴∠AOG=∠AOB+∠BOG=90°,
即△AOG是等腰直角三角形,
由勾股定理得:AG=
=
=2
,
即AC=2
+3.
故答案是:2
+3.
 解:在AC上截取CG=AB=3,连接OG,
解:在AC上截取CG=AB=3,连接OG,∵四边形BCEF是正方形,∠BAC=90°,
∴OB=OC,∠BAC=∠BOC=90°,
∴B、A、O、C四点共圆,
∴∠ABO=∠ACO,
在△BAO和△CGO中
|
∴△BAO≌△CGO(SAS),
∴OA=OG=2,∠AOB=∠COG,
∵∠BOC=∠COG+∠BOG=90°,
∴∠AOG=∠AOB+∠BOG=90°,
即△AOG是等腰直角三角形,
由勾股定理得:AG=
| AO2+OG2 |
| 22+22 |
| 2 |
即AC=2
| 2 |
故答案是:2
| 2 |
点评:本题主要考查对勾股定理,正方形的性质,直角三角形的性质,全等三角形的性质和判定等知识点的理解和掌握,能熟练地运用这些性质进行推理和计算是解此题的关键.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
 如图,AB=AC=4,P是BC上异于B、C的一点,则AP2+BP•PC的值是( )
如图,AB=AC=4,P是BC上异于B、C的一点,则AP2+BP•PC的值是( )| A、16 | B、20 | C、25 | D、30 |
 如图,在△ABC中,∠ABC=90°,∠C=40°,AC∥BD,那么∠ABD的度数为( )
如图,在△ABC中,∠ABC=90°,∠C=40°,AC∥BD,那么∠ABD的度数为( )| A、30° | B、40° |
| C、50° | D、60° |

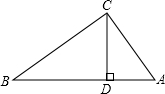 已知CD⊥AB,AC2=AD•AB,求证:
已知CD⊥AB,AC2=AD•AB,求证: