题目内容
 如图,在矩形ABCD中,AC与BD交于点O,若AB=3,AC=6,则∠AOD等于( )
如图,在矩形ABCD中,AC与BD交于点O,若AB=3,AC=6,则∠AOD等于( )| A、90° | B、100° |
| C、110° | D、120° |
考点:矩形的性质
专题:
分析:先根据矩形的对角线相等且互相平分得出OA=OB=
AC=3=AB,那么△OAB是等边三角形,根据等边三角形的性质得出∠AOB=60°,进而由邻补角定义求得∠AOD=120°.
| 1 |
| 2 |
解答:解:∵在矩形ABCD中,AC与BD交于点O,AC=6,
∴OA=OB=
AC=3,
∵AB=3,
∴OA=OB=AB,
∴△OAB是等边三角形,
∴∠AOB=60°,
∴∠AOD=180°-∠AOB=120°.
故选D.
∴OA=OB=
| 1 |
| 2 |
∵AB=3,
∴OA=OB=AB,
∴△OAB是等边三角形,
∴∠AOB=60°,
∴∠AOD=180°-∠AOB=120°.
故选D.
点评:本题考查了矩形的性质,等边三角形的判定与性质,邻补角定义,难度适中.得出△OAB是等边三角形是解题的关键.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案
相关题目
 如图,矩形ABCD的两条对角线交于点O,若∠AOD=120°,AB=6,则AC等于( )
如图,矩形ABCD的两条对角线交于点O,若∠AOD=120°,AB=6,则AC等于( )| A、8 | B、10 | C、12 | D、18 |
以下说法:①两点之间的所有连线中,线段最短;②相等的角是对顶角;③若AC=BC,则点C是线段AB的中点;④长方体是四棱柱;⑤不相交的两条直线叫做平行线;⑥过一点有且只有一条直线与已知直线垂直.其中正确的有( )
| A、1个 | B、2个 | C、3个 | D、4个 |
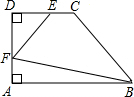 如图所示,在直角梯形ABCD中,∠A=∠D=90°,E、F分别是DC、DA边上,且DE=AF,已知DC=3,AD=4,AB=6,设DE=x,四边形EFBC的面积是S.
如图所示,在直角梯形ABCD中,∠A=∠D=90°,E、F分别是DC、DA边上,且DE=AF,已知DC=3,AD=4,AB=6,设DE=x,四边形EFBC的面积是S.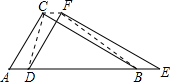 如图,△ABC中,∠ACB=90°,∠A=60°,AC=2.将△ABC沿射线AB向右平移得到△DEF,连接DC、CF、FB,在平移的过程中,有以下结论:①四边形ADFC始终是平行四边形;②以C、D、B、F为顶点的四边形面积始终等于2
如图,△ABC中,∠ACB=90°,∠A=60°,AC=2.将△ABC沿射线AB向右平移得到△DEF,连接DC、CF、FB,在平移的过程中,有以下结论:①四边形ADFC始终是平行四边形;②以C、D、B、F为顶点的四边形面积始终等于2