题目内容
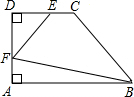 如图所示,在直角梯形ABCD中,∠A=∠D=90°,E、F分别是DC、DA边上,且DE=AF,已知DC=3,AD=4,AB=6,设DE=x,四边形EFBC的面积是S.
如图所示,在直角梯形ABCD中,∠A=∠D=90°,E、F分别是DC、DA边上,且DE=AF,已知DC=3,AD=4,AB=6,设DE=x,四边形EFBC的面积是S.(1)求S关于x的函数表达式和x的取值范围;
(2)如果S四边形EFBC=10,求DE的长度.
考点:直角梯形,一元二次方程的应用
专题:
分析:(1)根据四边形EFBC的面积S=S梯形ABCD-S△DEF-S△ABF列式整理即可,再根据CD的长度写出x的取值范围;
(2)根据S四边形EFBC=10列出方程,然后解一元二次方程即可.
(2)根据S四边形EFBC=10列出方程,然后解一元二次方程即可.
解答:解:(1)四边形EFBC的面积S=S梯形ABCD-S△DEF-S△ABF,
=
×(3+6)×4-
(4-x)•x-
×6•x,
=18-2x+
x2-3x,
=
x2-5x+18,
∵CD=3,
∴0<x<3;
(2)∵S四边形EFBC=10,
∴
x2-5x+18=10,
整理得,x2-10x+16=0,
解得x1=2,x2=8(舍去),
所以DE的长度为2.
=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
=18-2x+
| 1 |
| 2 |
=
| 1 |
| 2 |
∵CD=3,
∴0<x<3;
(2)∵S四边形EFBC=10,
∴
| 1 |
| 2 |
整理得,x2-10x+16=0,
解得x1=2,x2=8(舍去),
所以DE的长度为2.
点评:本题考查了直角梯形,三角形的面积,解一元二次方程,观察图形表示出四边形EFBC的面积是解题的关键.

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
 如图,在矩形ABCD中,AC与BD交于点O,若AB=3,AC=6,则∠AOD等于( )
如图,在矩形ABCD中,AC与BD交于点O,若AB=3,AC=6,则∠AOD等于( )| A、90° | B、100° |
| C、110° | D、120° |
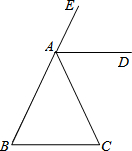 如图,AD是△ABC的外角∠EAC的平分线,且AD∥BC.
如图,AD是△ABC的外角∠EAC的平分线,且AD∥BC.