题目内容
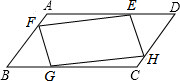 已知点E、F、G、H分别在AD、AB、BC、CD上,AD∥BC,AB∥CD,EF∥GH,FG∥EH,求证:△FAE≌△HCG.
已知点E、F、G、H分别在AD、AB、BC、CD上,AD∥BC,AB∥CD,EF∥GH,FG∥EH,求证:△FAE≌△HCG.考点:全等三角形的判定
专题:证明题
分析:延长FE交CD的延长线于M,根据两直线平行,内错角相等可得∠AFE=∠M,两直线平行,同位角相等可得∠CHG=∠M,从而得到∠AFE=∠CHG,再判断出四边形ABCD和四边形EFGH是平行四边形,根据平行四边形的对角相等可得∠A=∠C,对边相等可得EF=GH,然后利用“角角边”证明即可.
解答: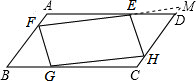 证明:如图,延长FE交CD的延长线于M,
证明:如图,延长FE交CD的延长线于M,
∵AB∥CD,
∴∠AFE=∠M,
∵EF∥GH,
∴∠CHG=∠M,
∴∠AFE=∠CHG,
∵AD∥BC,AB∥CD,
∴四边形ABCD是平行四边形,
∴∠A=∠C,
∵EF∥GH,FG∥EH,
∴四边形EFGH是平行四边形,
∴EF=GH,
在△FAE和△HCG中,
,
∴△FAE≌△HCG(AAS).
 证明:如图,延长FE交CD的延长线于M,
证明:如图,延长FE交CD的延长线于M,∵AB∥CD,
∴∠AFE=∠M,
∵EF∥GH,
∴∠CHG=∠M,
∴∠AFE=∠CHG,
∵AD∥BC,AB∥CD,
∴四边形ABCD是平行四边形,
∴∠A=∠C,
∵EF∥GH,FG∥EH,
∴四边形EFGH是平行四边形,
∴EF=GH,
在△FAE和△HCG中,
|
∴△FAE≌△HCG(AAS).
点评:本题考查了全等三角形的判定,平行四边形的判定与性质,平行线的性质,作辅助线并求出∠AFE=∠CHG是解题的关键.

练习册系列答案
 精英口算卡系列答案
精英口算卡系列答案 应用题点拨系列答案
应用题点拨系列答案
相关题目
 如图,已知∠1+∠2=180°,还需要添加条件∠3=
如图,已知∠1+∠2=180°,还需要添加条件∠3=