题目内容
 如图,已知∠1+∠2=180°,还需要添加条件∠3=
如图,已知∠1+∠2=180°,还需要添加条件∠3=考点:平行线的判定与性质
专题:
分析:求出∠2=∠4,推出AB∥EF推出∠3=∠ADE,求出∠ADE=∠B,根据三角形内角和定理求出即可.
解答:解:∠3=∠B,
理由是:∵∠1+∠4=180°,∠1+∠2=180°,
∴∠2=∠4,
∴AB∥EF,
∴∠3=∠ADE,
∵∠3=∠B,
∴∠ADE=∠B,
∵∠AED+∠ADE+∠A=180°,∠C+∠B+∠A=180°,
∴∠AED=∠C,
故答案为:∠B.
理由是:∵∠1+∠4=180°,∠1+∠2=180°,
∴∠2=∠4,
∴AB∥EF,
∴∠3=∠ADE,
∵∠3=∠B,
∴∠ADE=∠B,
∵∠AED+∠ADE+∠A=180°,∠C+∠B+∠A=180°,
∴∠AED=∠C,
故答案为:∠B.
点评:本题考查了平行线的性质和判定和三角形内角和定理的应用,主要考查学生的推理能力.

练习册系列答案
相关题目
如果样本1,2,3,5,x的平均数是3,那么x的值为( )
| A、4 | B、5 | C、3 | D、2 |
 如图,四边形ABCD是平行四边形,顶点A、B的坐标分别是A(1,0),B(0,-2),顶点C、D在双曲线
如图,四边形ABCD是平行四边形,顶点A、B的坐标分别是A(1,0),B(0,-2),顶点C、D在双曲线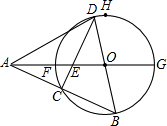 如图,点A在⊙O外,射线AO与⊙O交于F、G两点,点H在⊙O上,FH弧和GH弧为等弧,点D是FH弧上的一个动点(不运动至F),BD是⊙O的直径,连接AB,交⊙O于点C,连接CD,交AO于点E,且OA=
如图,点A在⊙O外,射线AO与⊙O交于F、G两点,点H在⊙O上,FH弧和GH弧为等弧,点D是FH弧上的一个动点(不运动至F),BD是⊙O的直径,连接AB,交⊙O于点C,连接CD,交AO于点E,且OA=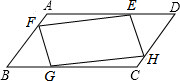 已知点E、F、G、H分别在AD、AB、BC、CD上,AD∥BC,AB∥CD,EF∥GH,FG∥EH,求证:△FAE≌△HCG.
已知点E、F、G、H分别在AD、AB、BC、CD上,AD∥BC,AB∥CD,EF∥GH,FG∥EH,求证:△FAE≌△HCG.