题目内容
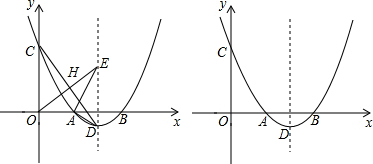
如图,抛物线y=
(x-3)2-1与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C,顶点为D.
(1)求点A,B,D的坐标;
(2)连接CD,过原点O作OE⊥CD,垂足为H,OE与抛物线的对称轴交于点E,连接AE,AD,求证:∠AEO=∠ADC;
(3)以(2)中的点E为圆心,1为半径画圆,在对称轴右侧的抛物线上有一动点P,过点P作⊙E的切线,切点为Q,当PQ的长最小时,求点P的坐标,并直接写出点Q的坐标.
| 1 |
| 2 |
(1)求点A,B,D的坐标;
(2)连接CD,过原点O作OE⊥CD,垂足为H,OE与抛物线的对称轴交于点E,连接AE,AD,求证:∠AEO=∠ADC;
(3)以(2)中的点E为圆心,1为半径画圆,在对称轴右侧的抛物线上有一动点P,过点P作⊙E的切线,切点为Q,当PQ的长最小时,求点P的坐标,并直接写出点Q的坐标.

考点:二次函数综合题
专题:代数几何综合题,压轴题
分析:(1)根据二次函数性质,求出点A、B、D的坐标;
(2)如何证明∠AEO=∠ADC?如答图1所示,我们观察到在△EFH与△ADF中:∠EHF=90°,有一对对顶角相等;因此只需证明∠EAD=90°即可,即△ADE为直角三角形,由此我们联想到勾股定理的逆定理.分别求出△ADE三边的长度,再利用勾股定理的逆定理证明它是直角三角形,由此问题解决;
(3)依题意画出图形,如答图2所示.由⊙E的半径为1,根据切线性质及勾股定理,得PQ2=EP2-1,要使切线长PQ最小,只需EP长最小,即EP2最小.利用二次函数性质求出EP2最小时点P的坐标,并进而求出点Q的坐标.
(2)如何证明∠AEO=∠ADC?如答图1所示,我们观察到在△EFH与△ADF中:∠EHF=90°,有一对对顶角相等;因此只需证明∠EAD=90°即可,即△ADE为直角三角形,由此我们联想到勾股定理的逆定理.分别求出△ADE三边的长度,再利用勾股定理的逆定理证明它是直角三角形,由此问题解决;
(3)依题意画出图形,如答图2所示.由⊙E的半径为1,根据切线性质及勾股定理,得PQ2=EP2-1,要使切线长PQ最小,只需EP长最小,即EP2最小.利用二次函数性质求出EP2最小时点P的坐标,并进而求出点Q的坐标.
解答:(1)解:顶点D的坐标为(3,-1).
令y=0,得
(x-3)2-1=0,
解得:x1=3+
,x2=3-
,
∵点A在点B的左侧,
∴A(3-
,0),B(3+
,0).
(2)证明:如答图1,过顶点D作DG⊥y轴于点G,则G(0,-1),GD=3.

令x=0,得y=
,
∴C(0,
).
∴CG=OC+OG=
+1=
,
∴tan∠DCG=
.
设对称轴交x轴于点M,则OM=3,DM=1,AM=3-(3-
)=
.
由OE⊥CD,易知∠EOM=∠DCG.
∴tan∠EOM=tan∠DCG=
=
,
解得EM=2,
∴DE=EM+DM=3.
在Rt△AEM中,AM=
,EM=2,由勾股定理得:AE=
;
在Rt△ADM中,AM=
,DM=1,由勾股定理得:AD=
.
∵AE2+AD2=6+3=9=DE2,
∴△ADE为直角三角形,∠EAD=90°.
设AE交CD于点F,
∵∠AEO+∠EFH=90°,∠ADC+AFD=90°,∠EFH=∠AFD(对顶角相等),
∴∠AEO=∠ADC.
(3)解:依题意画出图形,如答图2所示:

由⊙E的半径为1,根据切线性质及勾股定理,得PQ2=EP2-1,
要使切线长PQ最小,只需EP长最小,即EP2最小.
设点P坐标为(x,y),由勾股定理得:EP2=(x-3)2+(y-2)2.
∵y=
(x-3)2-1,
∴(x-3)2=2y+2.
∴EP2=2y+2+(y-2)2=(y-1)2+5
当y=1时,EP2有最小值,最小值为5.
将y=1代入y=
(x-3)2-1,得
(x-3)2-1=1,
解得:x1=1,x2=5.
又∵点P在对称轴右侧的抛物线上,
∴x1=1舍去.
∴P(5,1).
∵△EQ2P3为直角三角形,
∴过点Q2作x轴的平行线,再分别过点E,P向其作垂线,垂足分别为M点和N点.
由切割线定理得到Q2P=Q1P=2,EQ2=1
设点Q2的坐标为(m,n)
则在Rt△MQ2E和Rt△Q2NP中建立勾股方程,即(m-3)2+(n-2)2=1①,(5-m)2+(n-1)2=4②
①-②得n=2m-5③
将③代入到①得到
m1=3(舍,为Q1)
m2=
再将m=
代入③得n=
,
∴Q2(
,
)
此时点Q坐标为(3,1)或(
,
).
令y=0,得
| 1 |
| 2 |
解得:x1=3+
| 2 |
| 2 |
∵点A在点B的左侧,
∴A(3-
| 2 |
| 2 |
(2)证明:如答图1,过顶点D作DG⊥y轴于点G,则G(0,-1),GD=3.

令x=0,得y=
| 7 |
| 2 |
∴C(0,
| 7 |
| 2 |
∴CG=OC+OG=
| 7 |
| 2 |
| 9 |
| 2 |
∴tan∠DCG=
| 2 |
| 3 |
设对称轴交x轴于点M,则OM=3,DM=1,AM=3-(3-
| 2 |
| 2 |
由OE⊥CD,易知∠EOM=∠DCG.
∴tan∠EOM=tan∠DCG=
| EM |
| OM |
| 2 |
| 3 |
解得EM=2,
∴DE=EM+DM=3.
在Rt△AEM中,AM=
| 2 |
| 6 |
在Rt△ADM中,AM=
| 2 |
| 3 |
∵AE2+AD2=6+3=9=DE2,
∴△ADE为直角三角形,∠EAD=90°.
设AE交CD于点F,
∵∠AEO+∠EFH=90°,∠ADC+AFD=90°,∠EFH=∠AFD(对顶角相等),
∴∠AEO=∠ADC.
(3)解:依题意画出图形,如答图2所示:

由⊙E的半径为1,根据切线性质及勾股定理,得PQ2=EP2-1,
要使切线长PQ最小,只需EP长最小,即EP2最小.
设点P坐标为(x,y),由勾股定理得:EP2=(x-3)2+(y-2)2.
∵y=
| 1 |
| 2 |
∴(x-3)2=2y+2.
∴EP2=2y+2+(y-2)2=(y-1)2+5
当y=1时,EP2有最小值,最小值为5.
将y=1代入y=
| 1 |
| 2 |
| 1 |
| 2 |
解得:x1=1,x2=5.
又∵点P在对称轴右侧的抛物线上,
∴x1=1舍去.
∴P(5,1).
∵△EQ2P3为直角三角形,
∴过点Q2作x轴的平行线,再分别过点E,P向其作垂线,垂足分别为M点和N点.
由切割线定理得到Q2P=Q1P=2,EQ2=1
设点Q2的坐标为(m,n)
则在Rt△MQ2E和Rt△Q2NP中建立勾股方程,即(m-3)2+(n-2)2=1①,(5-m)2+(n-1)2=4②
①-②得n=2m-5③
将③代入到①得到
m1=3(舍,为Q1)
m2=
| 19 |
| 5 |
再将m=
| 19 |
| 5 |
| 13 |
| 5 |
∴Q2(
| 19 |
| 5 |
| 13 |
| 5 |
此时点Q坐标为(3,1)或(
| 19 |
| 5 |
| 13 |
| 5 |
点评:本题是二次函数压轴题,涉及考点众多,难度较大.第(2)问中,注意观察图形,将问题转化为证明△ADE为直角三角形的问题,综合运用勾股定理及其逆定理、三角函数(或相似形)求解;第(3)问中,解题关键是将最值问题转化为求EP2最小值的问题,注意解答中求EP2最小值的具体方法.

练习册系列答案
相关题目
如果样本1,2,3,5,x的平均数是3,那么x的值为( )
| A、4 | B、5 | C、3 | D、2 |
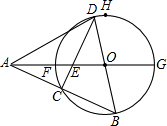 如图,点A在⊙O外,射线AO与⊙O交于F、G两点,点H在⊙O上,FH弧和GH弧为等弧,点D是FH弧上的一个动点(不运动至F),BD是⊙O的直径,连接AB,交⊙O于点C,连接CD,交AO于点E,且OA=
如图,点A在⊙O外,射线AO与⊙O交于F、G两点,点H在⊙O上,FH弧和GH弧为等弧,点D是FH弧上的一个动点(不运动至F),BD是⊙O的直径,连接AB,交⊙O于点C,连接CD,交AO于点E,且OA=
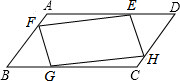 已知点E、F、G、H分别在AD、AB、BC、CD上,AD∥BC,AB∥CD,EF∥GH,FG∥EH,求证:△FAE≌△HCG.
已知点E、F、G、H分别在AD、AB、BC、CD上,AD∥BC,AB∥CD,EF∥GH,FG∥EH,求证:△FAE≌△HCG. 邻边不相等的平行四边形纸片,剪去一个菱形,余下一个四边形,称为第一次操作,在余下的四边形纸片中再剪去一个菱形,余下一个四边形,称为第二次操作,…依此类推,若第n次余下的四边形是菱形,则称原平行四边形为n阶准菱形,如图1,?ABCD中,若AB=1,BC=2,则?ABCD为1阶准菱形.
邻边不相等的平行四边形纸片,剪去一个菱形,余下一个四边形,称为第一次操作,在余下的四边形纸片中再剪去一个菱形,余下一个四边形,称为第二次操作,…依此类推,若第n次余下的四边形是菱形,则称原平行四边形为n阶准菱形,如图1,?ABCD中,若AB=1,BC=2,则?ABCD为1阶准菱形.