题目内容
1.若关于x的方程x2-3x+2a=0有两个不相等的实数根,则关于x的一元二次方程x2+3x+2a=0的根的情况是有两个不相等的实数根.分析 先利用判别式的意义,由关于x的方程x2-3x+2a=0有两个不相等的实数根得到△=(-3)2-4•2a>0,解得a<$\frac{9}{8}$,再计算方程x2+3x+2a=0的判别式得到△′=32-4•2a=9+8a,然后根据a的范围可判定△′>0,于是利用判别式的意义可判断此方程根的情况.
解答 解:∵关于x的方程x2-3x+2a=0有两个不相等的实数根,
∴△=(-3)2-4•2a>0,解得a<$\frac{9}{8}$,
∵△′=32-4•2a=9+8a,
∴△′>0,
∴关于x的一元二次方程x2+3x+2a=0有两个不相等的实数根.
故答案为有两个不相等的实数根.
点评 本题考查了根与系数的关系:一元二次方程ax2+bx+c=0(a≠0)的根与△=b2-4ac有如下关系:当△>0时,方程有两个不相等的两个实数根;当△=0时,方程有两个相等的两个实数根;当△<0时,方程无实数根.

练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目
13.若a2-2a-3=0,代数式$\frac{1}{a(a-2)}$的值是( )
| A. | -$\frac{1}{3}$ | B. | $\frac{1}{3}$ | C. | -3 | D. | 3 |
10.某班学生分组做抛掷同一型号的一枚图钉的实验,大量重复实验的结果统计如下表:
(顶尖朝上频率精确到 0.001)
根据表格中的信息,估计掷一枚这样的图钉落地后顶尖朝上的概率为0.530.
(顶尖朝上频率精确到 0.001)
| 累计实验次数 | 100 | 200 | 300 | 400 | 500 |
| 顶尖朝上次数 | 55 | 109 | 161 | 211 | 269 |
| 顶尖朝上频率 | 0.550 | 0.545 | 0.536 | 0.528 | 0.538 |
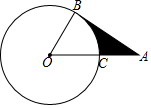 如图,AB是⊙O的切线,切点为B,AO交⊙O于点C,且AC=OC,若⊙O的半径是4,则阴影部分面积是8$\sqrt{3}$-$\frac{8}{3}$π.
如图,AB是⊙O的切线,切点为B,AO交⊙O于点C,且AC=OC,若⊙O的半径是4,则阴影部分面积是8$\sqrt{3}$-$\frac{8}{3}$π. 如图是由三个直角三角形组成的梯形,根据图形,写出一个正确的等式c2=a2+b2.
如图是由三个直角三角形组成的梯形,根据图形,写出一个正确的等式c2=a2+b2.