题目内容
12.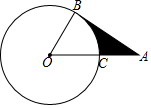 如图,AB是⊙O的切线,切点为B,AO交⊙O于点C,且AC=OC,若⊙O的半径是4,则阴影部分面积是8$\sqrt{3}$-$\frac{8}{3}$π.
如图,AB是⊙O的切线,切点为B,AO交⊙O于点C,且AC=OC,若⊙O的半径是4,则阴影部分面积是8$\sqrt{3}$-$\frac{8}{3}$π.
分析 直接利用切线的性质结合勾股定理得出AB的长,再利用锐角三角函数关系得出∠BOC的度数,结合阴影部分的面积为:S△OBA-S扇形BOC求出即可.
解答 解:∵AB是⊙O的切线,切点为B,
∴∠OBBA=90°,
∵AC=OC,⊙O的半径为4,
∴AC=4,AB=4$\sqrt{3}$,
∴∠A=30°,则∠BOC=60°,
∴图中阴影部分的面积为:S△OBA-S扇形BOC=$\frac{1}{2}$×BO×AB-$\frac{60π×{4}^{2}}{360}$=8$\sqrt{3}$-$\frac{8}{3}$π,
故答案为:8$\sqrt{3}$-$\frac{8}{3}$π.
点评 此题主要考查了扇形面积公式以及切线的性质,得出阴影部分的面积为:S△OBA-S扇形BOC是解题关键.

练习册系列答案
相关题目
3.甲、乙两名运动员进行射击练习,每人射击5次,成绩(单位:环)如下表所示:下列说法错误的是( )
| 第1次 | 第2次 | 第3次 | 第4次 | 第5次 | 平均成绩 | |
| 甲 | 7 | ▲ | 8 | 10 | 8 | 8 |
| 乙 | 7 | 8 | 8 | 9 | 8 | ▲ |
| A. | 甲运动员的第2次射击成绩为7环 | B. | 乙运动员的平均射击成绩为8环 | ||
| C. | 甲运动员这5次射击成绩的方差为6 | D. | 乙运动员的成绩更稳定 |
20.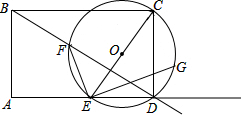 如图,矩形ABCD的边AB=3cm,AD=4cm,点E从点A出发,沿射线AD移动,以CE为直径作⊙O,点F为⊙O与射线BD的公共点,连接EF,过点E作EG⊥EF,交⊙O于点G,当⊙O与射线BD相切时,点E停止移动,则在运动过程中点G移动路程的长为( )
如图,矩形ABCD的边AB=3cm,AD=4cm,点E从点A出发,沿射线AD移动,以CE为直径作⊙O,点F为⊙O与射线BD的公共点,连接EF,过点E作EG⊥EF,交⊙O于点G,当⊙O与射线BD相切时,点E停止移动,则在运动过程中点G移动路程的长为( )
 如图,矩形ABCD的边AB=3cm,AD=4cm,点E从点A出发,沿射线AD移动,以CE为直径作⊙O,点F为⊙O与射线BD的公共点,连接EF,过点E作EG⊥EF,交⊙O于点G,当⊙O与射线BD相切时,点E停止移动,则在运动过程中点G移动路程的长为( )
如图,矩形ABCD的边AB=3cm,AD=4cm,点E从点A出发,沿射线AD移动,以CE为直径作⊙O,点F为⊙O与射线BD的公共点,连接EF,过点E作EG⊥EF,交⊙O于点G,当⊙O与射线BD相切时,点E停止移动,则在运动过程中点G移动路程的长为( )| A. | 4cm | B. | $\frac{15}{4}$cm | C. | $\frac{108}{25}$cm | D. | $\frac{12}{5}$cm |
4.若分式-$\frac{1}{x-2}$有意义,则x的取值范围是( )
| A. | x>2 | B. | x≠2 | C. | x=2 | D. | x<2 |
