题目内容
8.已知关于x的方程$\frac{a-x}{2}$=$\frac{bx-3}{3}$的解是方程$\frac{1}{4}$x-$\frac{1}{2}$=0的解,求$\frac{a}{b}$+$\frac{b}{a}$的值.分析 根据解方程,可得x的值,根据同解方程,可得a、b的关系,根据等式的性质,可得a:b的值,再根据分数的加法,可得答案.
解答 解:由$\frac{1}{4}$x-$\frac{1}{2}$=0,解得x=2.
将x=2代入$\frac{a-x}{2}$=$\frac{bx-3}{3}$,得
$\frac{a-2}{2}$=$\frac{2b-3}{3}$.
两边都乘以6,得
3a-6=4b-6.
两边都加6,得
3a=4b.
两边都除以3b,得
$\frac{a}{b}$=$\frac{4}{3}$.
$\frac{a}{b}$+$\frac{b}{a}$=$\frac{4}{3}$+$\frac{3}{4}$=$\frac{16}{12}$+$\frac{9}{12}$=$\frac{25}{16}$.
点评 本题考查了同解方程,利用通解方程的出关于a,b的方程是解题关键,又利用了等式的性质.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
20.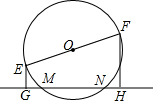 如图,EF为⊙O的直径,EF=10cm,弦NN=6cm,则E、F两点到直线MN的距离之和等于( )
如图,EF为⊙O的直径,EF=10cm,弦NN=6cm,则E、F两点到直线MN的距离之和等于( )
 如图,EF为⊙O的直径,EF=10cm,弦NN=6cm,则E、F两点到直线MN的距离之和等于( )
如图,EF为⊙O的直径,EF=10cm,弦NN=6cm,则E、F两点到直线MN的距离之和等于( )| A. | 12cm | B. | 8cm | C. | 6cm | D. | 3cm |
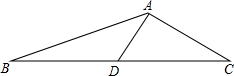 如图,在△ABC中,已知AB=13cm,AC=5cm,C边上的中线AD=6cm,求以BC为边长的正方形的面积.
如图,在△ABC中,已知AB=13cm,AC=5cm,C边上的中线AD=6cm,求以BC为边长的正方形的面积. 如图,在△ABA1中,∠B=20°,AB=A1B,在A1B上取一点B1,延长AA1到A2,使得A1A2=A1B1,连接A2B1,在A2B1上取一点B2,延长A1A2到A3,使得A2A3=A2B2;…,按此作法进行下去,∠A2015A2016B2015的度数为$\frac{80°}{{2}^{2015}}$.
如图,在△ABA1中,∠B=20°,AB=A1B,在A1B上取一点B1,延长AA1到A2,使得A1A2=A1B1,连接A2B1,在A2B1上取一点B2,延长A1A2到A3,使得A2A3=A2B2;…,按此作法进行下去,∠A2015A2016B2015的度数为$\frac{80°}{{2}^{2015}}$.