题目内容
10.若a+b=-3,ab=1.求$\frac{1}{2}$a3b+a2b2+$\frac{1}{2}$ab3的值.分析 先把原式提取公因式后,再利用完全平方公式分解,最后把各自的值代入计算即可.
解答 解:∵a+b=-3,ab=1
∴$\frac{1}{2}$a3b+a2b2+$\frac{1}{2}$ab3=$\frac{1}{2}$ab(a2+2ab+b2)=$\frac{1}{2}$ab(a+b)2=$\frac{1}{2}$×1×(-3)2=$\frac{9}{2}$.
点评 此题考查了因式分解,用到的知识点是提公因式法和公式法,熟练掌握因式分解的方法是解本题的关键.

练习册系列答案
相关题目
5.若a>b,则下列式子正确的是( )
| A. | -0.5a>-0.5b | B. | 0.5a>0.5b | C. | a+c<b+c | D. | a-c<b-c |
15.试计算|3-8|×(-2)的值为( )
| A. | 10 | B. | 7 | C. | -10 | D. | -7 |
20.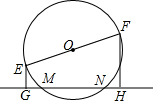 如图,EF为⊙O的直径,EF=10cm,弦NN=6cm,则E、F两点到直线MN的距离之和等于( )
如图,EF为⊙O的直径,EF=10cm,弦NN=6cm,则E、F两点到直线MN的距离之和等于( )
 如图,EF为⊙O的直径,EF=10cm,弦NN=6cm,则E、F两点到直线MN的距离之和等于( )
如图,EF为⊙O的直径,EF=10cm,弦NN=6cm,则E、F两点到直线MN的距离之和等于( )| A. | 12cm | B. | 8cm | C. | 6cm | D. | 3cm |
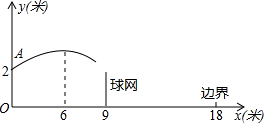 如图,排球运动员站在点O处练习发球,将球从点O正上方2米的点A处发出把球看成点,其运行的高度y(米)与运行的水平距离x(米)满足关系式y=a(x-6)2+2.6,已知球网与点O的水平距离为9米,高度为2.43米,球场的边界距点O的水平距离为18米.
如图,排球运动员站在点O处练习发球,将球从点O正上方2米的点A处发出把球看成点,其运行的高度y(米)与运行的水平距离x(米)满足关系式y=a(x-6)2+2.6,已知球网与点O的水平距离为9米,高度为2.43米,球场的边界距点O的水平距离为18米.