题目内容
17. 如图所示,若∠A+∠B+∠C+∠D+∠E+∠F=660°,求∠G+∠H的度数.
如图所示,若∠A+∠B+∠C+∠D+∠E+∠F=660°,求∠G+∠H的度数.
分析 根据三角形内角和定理得到∠G+∠H=∠DAF+∠DFA,根据n边形的内角和为(n-2)×180°求出∠A+∠B+∠C+∠D+∠E+∠F+∠DAF+∠DFA的度数,得到答案.
解答  解:连接AF,
解:连接AF,
∵∠GDH=∠ADF,
∴∠G+∠H=∠DAF+∠DFA,
∵∠A+∠B+∠C+∠D+∠E+∠F+∠DAF+∠DFA=(6-2)×180°=720°,又∠A+∠B+∠C+∠D+∠E+∠F=660°,
∴∠DAF+∠DFA=720°-660°=60°,
则∠G+∠H=60°.
点评 本题考查的是多边形的内角和定理和三角形的外角的性质,掌握n边形的内角和为(n-2)×180°是解题的关键.

练习册系列答案
相关题目
6.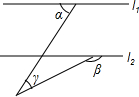 如图,l1∥l2,则下列式子成立的是( )
如图,l1∥l2,则下列式子成立的是( )
 如图,l1∥l2,则下列式子成立的是( )
如图,l1∥l2,则下列式子成立的是( )| A. | ∠α+∠β+∠γ=180° | B. | ∠α+∠β-∠γ=180° | C. | ∠β+∠γ-∠α=180° | D. | ∠α-∠β+∠γ=180° |
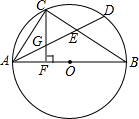 如图,AB是⊙O的直径,D是$\widehat{AB}$上一点,C是弧$\widehat{AD}$的中点,AD、BC相交于E,CF⊥AB,F为垂足,CF交AD于G,求证:CG=EG.
如图,AB是⊙O的直径,D是$\widehat{AB}$上一点,C是弧$\widehat{AD}$的中点,AD、BC相交于E,CF⊥AB,F为垂足,CF交AD于G,求证:CG=EG.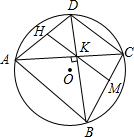 如图.在⊙O的内接四边形ABCD中,AC⊥BD,垂足为K,M是BC的中点,直线MK交AD于点H.KH与AD有怎样的位置关系?为什么?
如图.在⊙O的内接四边形ABCD中,AC⊥BD,垂足为K,M是BC的中点,直线MK交AD于点H.KH与AD有怎样的位置关系?为什么? 已知:如图,∠BCA=∠DAC.求证:∠B与∠DAB互补.
已知:如图,∠BCA=∠DAC.求证:∠B与∠DAB互补.