题目内容
8.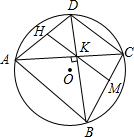 如图.在⊙O的内接四边形ABCD中,AC⊥BD,垂足为K,M是BC的中点,直线MK交AD于点H.KH与AD有怎样的位置关系?为什么?
如图.在⊙O的内接四边形ABCD中,AC⊥BD,垂足为K,M是BC的中点,直线MK交AD于点H.KH与AD有怎样的位置关系?为什么?
分析 根据直角三角形斜边中线的性质得出KM=CM,进而得出∠KCB=∠MKC,因为∠KBC+∠KCB=90°,∠AKH=∠CKM,∠HAK=∠KBC,即可证得∠AHK=90°.
解答 解:垂直,
理由:∵AC⊥BD,M是BC的中点,
∴KM=CM,∠KBC+∠KCB=90°,
∴∠KCB=∠MKC,
∵∠AKH=∠CKM,
∴∠KCB=∠AKH,
∵∠HAK=∠KBC,
∴∠HAK+∠AKH=90°,
∴∠AHK=90°,
∴KH⊥AD.
点评 本题考查了圆周角定理的应用,直角三角形斜边中线的性质,熟练掌握和应用性质定理是解题的关键.

练习册系列答案
相关题目
18.在平面内有A、B两点,若以B点为原点建立平面直角坐标系,则点A的坐标为(2,5),若以A点为原点建立平面直角坐标系,则点B的坐标为( )
| A. | (-2,-5) | B. | (-2,5) | C. | (2,-5) | D. | (2,5) |
19.下列银行标志中是轴对称图形的个数有( )


| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
16.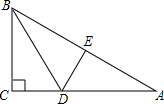 如图,在△ABC中,∠C=90°,BD平分∠ABC交AC于D,DE是AB的垂直平分线,DE=$\frac{1}{2}$BD,DE=1.5cm,则AC等于( )
如图,在△ABC中,∠C=90°,BD平分∠ABC交AC于D,DE是AB的垂直平分线,DE=$\frac{1}{2}$BD,DE=1.5cm,则AC等于( )
 如图,在△ABC中,∠C=90°,BD平分∠ABC交AC于D,DE是AB的垂直平分线,DE=$\frac{1}{2}$BD,DE=1.5cm,则AC等于( )
如图,在△ABC中,∠C=90°,BD平分∠ABC交AC于D,DE是AB的垂直平分线,DE=$\frac{1}{2}$BD,DE=1.5cm,则AC等于( )| A. | 3cm | B. | 7.5cm | C. | 6cm | D. | 4.5cm |
12.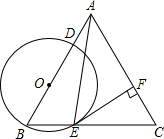 如图,在等边△ABC中,点O在边AB上,⊙O过点B且分别与边AB、BC相交于点D、E、F是AC上的点,判断下列说法错误的是( )
如图,在等边△ABC中,点O在边AB上,⊙O过点B且分别与边AB、BC相交于点D、E、F是AC上的点,判断下列说法错误的是( )
 如图,在等边△ABC中,点O在边AB上,⊙O过点B且分别与边AB、BC相交于点D、E、F是AC上的点,判断下列说法错误的是( )
如图,在等边△ABC中,点O在边AB上,⊙O过点B且分别与边AB、BC相交于点D、E、F是AC上的点,判断下列说法错误的是( )| A. | 若EF⊥AC,则EF是⊙O的切线 | B. | 若EF是⊙O的切线,则EF⊥AC | ||
| C. | 若BE=EC,则AC是⊙O的切线 | D. | 若BE=$\frac{\sqrt{3}}{2}$EC,则AC是⊙O的切线 |
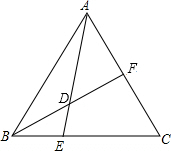 如图,在△ABC中,E是BC上一点,EC=2BE,点F是AC的中点,若S△ABC=12,求S△ADF-S△BED的值.
如图,在△ABC中,E是BC上一点,EC=2BE,点F是AC的中点,若S△ABC=12,求S△ADF-S△BED的值.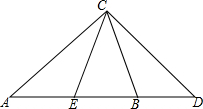 如图,点A、E、B、D在同一条直线上,AE=DB,∠A=∠D,∠CED=∠CBA,试判断△ACE与△CDB是否全等,并说明理由.
如图,点A、E、B、D在同一条直线上,AE=DB,∠A=∠D,∠CED=∠CBA,试判断△ACE与△CDB是否全等,并说明理由. 如图,BC∥DF,∠B=45°,∠A=25°,求∠D的度数.
如图,BC∥DF,∠B=45°,∠A=25°,求∠D的度数. 如图所示,若∠A+∠B+∠C+∠D+∠E+∠F=660°,求∠G+∠H的度数.
如图所示,若∠A+∠B+∠C+∠D+∠E+∠F=660°,求∠G+∠H的度数.