题目内容
5. 已知:如图,∠BCA=∠DAC.求证:∠B与∠DAB互补.
已知:如图,∠BCA=∠DAC.求证:∠B与∠DAB互补.
分析 根据平行线的判定得出AD∥BC,根据平行线的性质得出即可.
解答 证明:∵∠BCA=∠DAC,
∴AD∥BC,
∴∠B+∠DAB=180°,
即∠B与∠DAB互补.
点评 本题考查了平行线的性质和判定的应用,能推出AD∥BC是解此题的关键,注意:①内错角相等,两直线平行,②两直线平行,同旁内角互补.

练习册系列答案
相关题目
16.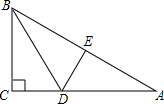 如图,在△ABC中,∠C=90°,BD平分∠ABC交AC于D,DE是AB的垂直平分线,DE=$\frac{1}{2}$BD,DE=1.5cm,则AC等于( )
如图,在△ABC中,∠C=90°,BD平分∠ABC交AC于D,DE是AB的垂直平分线,DE=$\frac{1}{2}$BD,DE=1.5cm,则AC等于( )
 如图,在△ABC中,∠C=90°,BD平分∠ABC交AC于D,DE是AB的垂直平分线,DE=$\frac{1}{2}$BD,DE=1.5cm,则AC等于( )
如图,在△ABC中,∠C=90°,BD平分∠ABC交AC于D,DE是AB的垂直平分线,DE=$\frac{1}{2}$BD,DE=1.5cm,则AC等于( )| A. | 3cm | B. | 7.5cm | C. | 6cm | D. | 4.5cm |
14. 如图,已知l1∥l2,则下列不等式一定正确的是( )
如图,已知l1∥l2,则下列不等式一定正确的是( )
 如图,已知l1∥l2,则下列不等式一定正确的是( )
如图,已知l1∥l2,则下列不等式一定正确的是( )| A. | ∠2>∠3 | B. | ∠3>∠2 | C. | ∠1>∠2 | D. | ∠1>∠2+∠3 |
9.如图,菱形ABCD中,AB=2,∠C=60°,我们把菱形ABCD的对称中心O称作菱形的中心,菱形ABCD在直线L上向右作无滑动的翻滚,每绕着一个顶点旋转60°叫做一次操作,则经过2013次这样的操作菱形中心O所经过的路径总长为( )
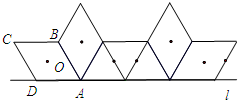

| A. | $\frac{{671(\sqrt{3}+1)}}{3}$π | B. | $\frac{{671(2\sqrt{3}+1)}}{2}$π | C. | $\frac{{671(2\sqrt{3}+1)}}{3}$π | D. | $\frac{{1342\sqrt{3}}}{3}$π |
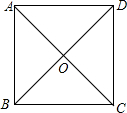 如图是一个边长为a的正方形.两条对角线AC与BD相交于O.观察此图并回答下面问题:
如图是一个边长为a的正方形.两条对角线AC与BD相交于O.观察此图并回答下面问题: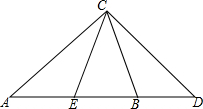 如图,点A、E、B、D在同一条直线上,AE=DB,∠A=∠D,∠CED=∠CBA,试判断△ACE与△CDB是否全等,并说明理由.
如图,点A、E、B、D在同一条直线上,AE=DB,∠A=∠D,∠CED=∠CBA,试判断△ACE与△CDB是否全等,并说明理由. 如图,BC∥DF,∠B=45°,∠A=25°,求∠D的度数.
如图,BC∥DF,∠B=45°,∠A=25°,求∠D的度数. 如图所示,若∠A+∠B+∠C+∠D+∠E+∠F=660°,求∠G+∠H的度数.
如图所示,若∠A+∠B+∠C+∠D+∠E+∠F=660°,求∠G+∠H的度数.