题目内容
9.已知一个凸边形除了一个内角外,其余各内角和为1125°,求这个内角的度数及这个多边形的边数.分析 根据n边形的内角和是(n-2)•180°,可以得到内角和一定是180度的整数倍,即可求解.
解答 解:1125÷180=6$\frac{29}{36}$,则正多边形的边数是6+1+2=9边形.
∴内角和为:(9-2)×180°=1260°,
这个内角为:1260°-1125°=135°.
答:这个内角的度数为135°,这个多边形的边数为9.
点评 本题考查根据多边形的内角和计算公式求多边形的边数,掌握n边形的内角和是(n-2)•180°是解题的关键.

练习册系列答案
相关题目
19.下列银行标志中是轴对称图形的个数有( )


| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
14. 如图,已知l1∥l2,则下列不等式一定正确的是( )
如图,已知l1∥l2,则下列不等式一定正确的是( )
 如图,已知l1∥l2,则下列不等式一定正确的是( )
如图,已知l1∥l2,则下列不等式一定正确的是( )| A. | ∠2>∠3 | B. | ∠3>∠2 | C. | ∠1>∠2 | D. | ∠1>∠2+∠3 |
12.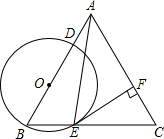 如图,在等边△ABC中,点O在边AB上,⊙O过点B且分别与边AB、BC相交于点D、E、F是AC上的点,判断下列说法错误的是( )
如图,在等边△ABC中,点O在边AB上,⊙O过点B且分别与边AB、BC相交于点D、E、F是AC上的点,判断下列说法错误的是( )
 如图,在等边△ABC中,点O在边AB上,⊙O过点B且分别与边AB、BC相交于点D、E、F是AC上的点,判断下列说法错误的是( )
如图,在等边△ABC中,点O在边AB上,⊙O过点B且分别与边AB、BC相交于点D、E、F是AC上的点,判断下列说法错误的是( )| A. | 若EF⊥AC,则EF是⊙O的切线 | B. | 若EF是⊙O的切线,则EF⊥AC | ||
| C. | 若BE=EC,则AC是⊙O的切线 | D. | 若BE=$\frac{\sqrt{3}}{2}$EC,则AC是⊙O的切线 |
 如图,BC∥DF,∠B=45°,∠A=25°,求∠D的度数.
如图,BC∥DF,∠B=45°,∠A=25°,求∠D的度数. 如图所示,若∠A+∠B+∠C+∠D+∠E+∠F=660°,求∠G+∠H的度数.
如图所示,若∠A+∠B+∠C+∠D+∠E+∠F=660°,求∠G+∠H的度数.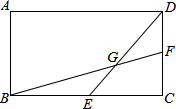 如图所示,长方形ABCD的长为a,宽为b,E、F分别为BC和CD的中点,连接BF、DE交于点G,则四边形ABGD的面积为$\frac{2}{3}$ab.
如图所示,长方形ABCD的长为a,宽为b,E、F分别为BC和CD的中点,连接BF、DE交于点G,则四边形ABGD的面积为$\frac{2}{3}$ab.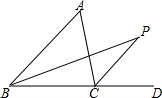 如图.在△ABC中,∠A=α.△ABC的内角平分线与外角平分线交于点P.且∠P=β.试探究图中α与β的关系.并说明理由.
如图.在△ABC中,∠A=α.△ABC的内角平分线与外角平分线交于点P.且∠P=β.试探究图中α与β的关系.并说明理由.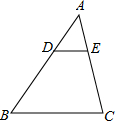 已知:如图,DE∥BC,AD=4cm,DE=2cm,BC=5cm.求:
已知:如图,DE∥BC,AD=4cm,DE=2cm,BC=5cm.求: