题目内容
6.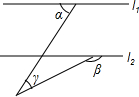 如图,l1∥l2,则下列式子成立的是( )
如图,l1∥l2,则下列式子成立的是( )| A. | ∠α+∠β+∠γ=180° | B. | ∠α+∠β-∠γ=180° | C. | ∠β+∠γ-∠α=180° | D. | ∠α-∠β+∠γ=180° |
分析 根据平行线的性质进行判断即可.
解答 解:因为l1∥l2,
所以∠α=(180°-∠β)+∠γ,
可得:∠α+∠β-∠γ=180°,
故选B
点评 此题考查平行线的性质,关键是根据平行线的性质得出∠α=(180°-∠β)+∠γ.

练习册系列答案
 教学练新同步练习系列答案
教学练新同步练习系列答案 课前课后同步练习系列答案
课前课后同步练习系列答案
相关题目
16.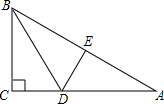 如图,在△ABC中,∠C=90°,BD平分∠ABC交AC于D,DE是AB的垂直平分线,DE=$\frac{1}{2}$BD,DE=1.5cm,则AC等于( )
如图,在△ABC中,∠C=90°,BD平分∠ABC交AC于D,DE是AB的垂直平分线,DE=$\frac{1}{2}$BD,DE=1.5cm,则AC等于( )
 如图,在△ABC中,∠C=90°,BD平分∠ABC交AC于D,DE是AB的垂直平分线,DE=$\frac{1}{2}$BD,DE=1.5cm,则AC等于( )
如图,在△ABC中,∠C=90°,BD平分∠ABC交AC于D,DE是AB的垂直平分线,DE=$\frac{1}{2}$BD,DE=1.5cm,则AC等于( )| A. | 3cm | B. | 7.5cm | C. | 6cm | D. | 4.5cm |
14. 如图,已知l1∥l2,则下列不等式一定正确的是( )
如图,已知l1∥l2,则下列不等式一定正确的是( )
 如图,已知l1∥l2,则下列不等式一定正确的是( )
如图,已知l1∥l2,则下列不等式一定正确的是( )| A. | ∠2>∠3 | B. | ∠3>∠2 | C. | ∠1>∠2 | D. | ∠1>∠2+∠3 |
12.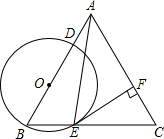 如图,在等边△ABC中,点O在边AB上,⊙O过点B且分别与边AB、BC相交于点D、E、F是AC上的点,判断下列说法错误的是( )
如图,在等边△ABC中,点O在边AB上,⊙O过点B且分别与边AB、BC相交于点D、E、F是AC上的点,判断下列说法错误的是( )
 如图,在等边△ABC中,点O在边AB上,⊙O过点B且分别与边AB、BC相交于点D、E、F是AC上的点,判断下列说法错误的是( )
如图,在等边△ABC中,点O在边AB上,⊙O过点B且分别与边AB、BC相交于点D、E、F是AC上的点,判断下列说法错误的是( )| A. | 若EF⊥AC,则EF是⊙O的切线 | B. | 若EF是⊙O的切线,则EF⊥AC | ||
| C. | 若BE=EC,则AC是⊙O的切线 | D. | 若BE=$\frac{\sqrt{3}}{2}$EC,则AC是⊙O的切线 |
9.如图,菱形ABCD中,AB=2,∠C=60°,我们把菱形ABCD的对称中心O称作菱形的中心,菱形ABCD在直线L上向右作无滑动的翻滚,每绕着一个顶点旋转60°叫做一次操作,则经过2013次这样的操作菱形中心O所经过的路径总长为( )
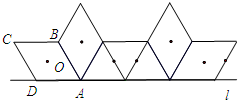

| A. | $\frac{{671(\sqrt{3}+1)}}{3}$π | B. | $\frac{{671(2\sqrt{3}+1)}}{2}$π | C. | $\frac{{671(2\sqrt{3}+1)}}{3}$π | D. | $\frac{{1342\sqrt{3}}}{3}$π |
10.下列函数中,是二次函数的是( )
| A. | y=-3x | B. | y=$\frac{4}{x}$ | C. | y=-2x-1 | D. | y=2x2 |
 如图所示,若∠A+∠B+∠C+∠D+∠E+∠F=660°,求∠G+∠H的度数.
如图所示,若∠A+∠B+∠C+∠D+∠E+∠F=660°,求∠G+∠H的度数.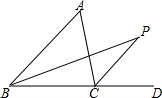 如图.在△ABC中,∠A=α.△ABC的内角平分线与外角平分线交于点P.且∠P=β.试探究图中α与β的关系.并说明理由.
如图.在△ABC中,∠A=α.△ABC的内角平分线与外角平分线交于点P.且∠P=β.试探究图中α与β的关系.并说明理由.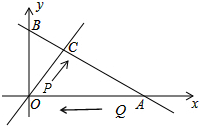 如图,直线m:y=kx(k>0)与直线n:y=-$\frac{\sqrt{3}}{3}$x+2$\sqrt{3}$相交于点C,点A、B为直线n与坐标轴的交点,∠COA=60°,点P从O点出发沿线段OC向点C匀速运动,速度为每秒1个单位,同时点Q从点A出发沿线段AO向点O匀速运动,速度为每秒2个单位,设运动时间为t秒.
如图,直线m:y=kx(k>0)与直线n:y=-$\frac{\sqrt{3}}{3}$x+2$\sqrt{3}$相交于点C,点A、B为直线n与坐标轴的交点,∠COA=60°,点P从O点出发沿线段OC向点C匀速运动,速度为每秒1个单位,同时点Q从点A出发沿线段AO向点O匀速运动,速度为每秒2个单位,设运动时间为t秒.