题目内容
16. 如图,在平面直角坐标系中,已知矩形ABCD的三个顶点B(4,0)C(8,0)D(8,8)抛物线y=ax2+bx过A,C两点,动点P从点A出发,沿线段AB向终点B运动,同时点Q从点C出发,沿线段CD向终点D运动,速度均为每秒1个单位长度,运动时间为t秒,过点P作PE⊥AB交AC于点E
如图,在平面直角坐标系中,已知矩形ABCD的三个顶点B(4,0)C(8,0)D(8,8)抛物线y=ax2+bx过A,C两点,动点P从点A出发,沿线段AB向终点B运动,同时点Q从点C出发,沿线段CD向终点D运动,速度均为每秒1个单位长度,运动时间为t秒,过点P作PE⊥AB交AC于点E(1)直接写出点A的坐标,并求出抛物线的解析式.
(2)过点E作EF⊥AD于点F,交抛物线于点G,当t为何值时,线段EG最长?
(3)连接EQ,在点P,Q运动的过程中,是否存在某个时刻,使得以C,E,Q为顶点的△CEQ为等腰三角形?如果存在,请直接写出相应的t值;如果不存在,请说明理由.
分析 (1)由于四边形ABCD为矩形,所以A点与D点纵坐标相同,A点与B点横坐标相同;再将A(4,8)、C(8,0)两点坐标分别代入y=ax2+bx,利用待定系数法即可求出抛物线的解析式;
(2)①根据相似三角形的性质求出点E的横坐标表达式即为点G的横坐标表达式,代入二次函数解析式,求出纵坐标表达式,将线段最值问题转化为二次函数最值问题解答;
②当△CEQ为等腰三角形时,可分EQ=QC,EC=CQ,EQ=EC三种情况讨论.根据两点间距离公式列出方程,解方程即可.
解答 解:(1)因为点B的横坐标为4,点D的纵坐标为8,AD∥x轴,AB∥y轴,所以点A的坐标为(4,8).
将A(4,8)、C(8,0)两点坐标分别代入y=ax2+bx,
得$\left\{\begin{array}{l}{16a+4b=8}\\{64a+8b=0}\end{array}\right.$,$\left\{\begin{array}{l}{a=-\frac{1}{2}}\\{b=4}\end{array}\right.$,
故抛物线的解析式为:y=-$\frac{1}{2}$x2+4x;
(2)①∵PE∥BC,
∴△APE∽△ABC,
∴$\frac{PE}{BC}$=$\frac{AP}{AB}$,即$\frac{PE}{4}$=$\frac{AP}{8}$,
∴PE=$\frac{1}{2}$AP=$\frac{1}{2}$t,PB=8-t.
∴点E的坐标为(4+$\frac{1}{2}$t,8-t).
∴点G的纵坐标为:-$\frac{1}{2}$(4+$\frac{1}{2}$t)2+4(4+$\frac{1}{2}$t)=-$\frac{1}{8}$t2+8.
∴EG=-$\frac{1}{8}$t2+8-(8-t)=-$\frac{1}{8}$t2+t.
∵-$\frac{1}{8}$<0,
∴当t=$\frac{-1}{2×(-\frac{1}{8})}$=4时,线段EG最长为2;
②∵Q(8,t),E(4+$\frac{1}{2}$t,8-t),C(8,0),
∴EQ2=($\frac{1}{2}$t-4)2+(8-2t)2,QC2=t2,EC2=(4+$\frac{1}{2}$t-8)2+(8-t)2.
当△CEQ为等腰三角形时,分三种情况: (Ⅰ)当EQ=QC时,
(Ⅰ)当EQ=QC时,
($\frac{1}{2}$t-4)2+(8-2t)2=t2,
整理得13t2-144t+320=0,
解得t=$\frac{40}{13}$或t=$\frac{104}{13}$=8(此时E、C重合,不能构成三角形,舍去);
(Ⅱ)当EC=CQ时,
(4+$\frac{1}{2}$t-8)2+(8-t)2=t2,
整理得t2-80t+320=0,
解得t=40-16$\sqrt{5}$,t=40+16$\sqrt{5}$>8(此时Q不在矩形的边上,舍去);
(Ⅲ)当EQ=EC时,
($\frac{1}{2}$t-4)2+(8-2t)2=(4+$\frac{1}{2}$t-8)2+(8-t)2,
解得t=0(此时Q、C重合,不能构成三角形,舍去)或t=$\frac{16}{3}$.
综上所述,存在时刻t1=$\frac{16}{3}$,t2=$\frac{40}{13}$,t3=40-16$\sqrt{5}$,能够使得以C,E,Q为顶点的△CEQ为等腰三角形.
点评 本题是二次函数的综合题型,其中涉及到利用待定系数法求抛物线的解析式,相似三角形的判定与性质,二次函数最值的求法,等腰三角形的性质,两点间的距离公式等知识,利用分类讨论及方程思想是解题的关键.

| A. | (-1,-2) | B. | (3,-2) | C. | (1,2) | D. | (-2,-3) |
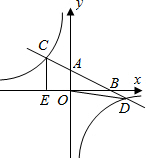 如图在平面直角坐标系xOy中,直线y1=-$\frac{1}{2}$x+2分别与x、y轴交于点B、A,与反比例函数y2=$\frac{k}{x}$(k≠0)的图象分别交于点C、D,CE⊥x轴于点E,OE=2.
如图在平面直角坐标系xOy中,直线y1=-$\frac{1}{2}$x+2分别与x、y轴交于点B、A,与反比例函数y2=$\frac{k}{x}$(k≠0)的图象分别交于点C、D,CE⊥x轴于点E,OE=2. 如图,四边形ABHK是边长为6的正方形,点C、D在边AB上,且AC=DB=1,点P是线段CD上的动点,分别以AP、PB为边在线段AB的同侧作正方形AMNP和正方形BRQP,
如图,四边形ABHK是边长为6的正方形,点C、D在边AB上,且AC=DB=1,点P是线段CD上的动点,分别以AP、PB为边在线段AB的同侧作正方形AMNP和正方形BRQP,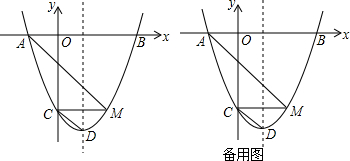
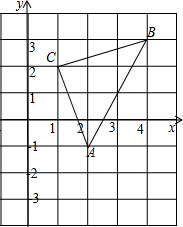 如图,直角坐标系中,△ABC的顶点都在网格点上,其中,C点坐标为(1,2).
如图,直角坐标系中,△ABC的顶点都在网格点上,其中,C点坐标为(1,2).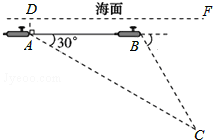 如图,一艘核潜艇在海面DF下600米A点处测得俯角为30°正前方的海底C点处有黑匣子,继续在同一深度直线航行1464米到B点处测得正前方C点处的俯角为55°.
如图,一艘核潜艇在海面DF下600米A点处测得俯角为30°正前方的海底C点处有黑匣子,继续在同一深度直线航行1464米到B点处测得正前方C点处的俯角为55°.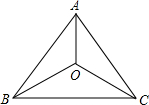 已知如图,在△ABC中,AB=AC,O是△ABC内一点,且OB=OC,求证:AO⊥BC.
已知如图,在△ABC中,AB=AC,O是△ABC内一点,且OB=OC,求证:AO⊥BC.