题目内容
5.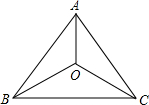 已知如图,在△ABC中,AB=AC,O是△ABC内一点,且OB=OC,求证:AO⊥BC.
已知如图,在△ABC中,AB=AC,O是△ABC内一点,且OB=OC,求证:AO⊥BC.
分析 延长AO交BC于点D,先证出△ABO≌△ACO,得出∠BAO=∠CAO,再根据三线合一的性质得出AO⊥BC即可.
解答 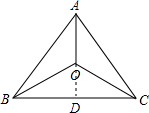 证明:延长AO交BC于点D,
证明:延长AO交BC于点D,
在△ABO和△ACO中,
$\left\{\begin{array}{l}{AB=AC}\\{AO=AO}\\{OB=OC}\end{array}\right.$,
∴△ABO≌△ACO(SSS),
∴∠BAO=∠CAO,
∵AB=AC,
∴AO⊥BC.
点评 本题考查了等腰三角形的性质,用到的知识点是全等三角形的判定和性质、等腰三角形三线合一的性质,关键是找出全等三角形.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
13.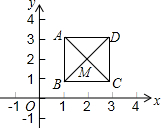 如图,已知正方形ABCD,顶点A(1,3)、B(1,1)、C(3,1).规定“把正方形ABCD先沿x轴翻折,再向左平移1个单位”为一次变换.如此这样,连续经过2015次变换后,正方形ABCD的对角线交点M的坐标变为( )
如图,已知正方形ABCD,顶点A(1,3)、B(1,1)、C(3,1).规定“把正方形ABCD先沿x轴翻折,再向左平移1个单位”为一次变换.如此这样,连续经过2015次变换后,正方形ABCD的对角线交点M的坐标变为( )
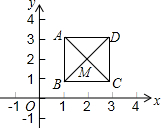 如图,已知正方形ABCD,顶点A(1,3)、B(1,1)、C(3,1).规定“把正方形ABCD先沿x轴翻折,再向左平移1个单位”为一次变换.如此这样,连续经过2015次变换后,正方形ABCD的对角线交点M的坐标变为( )
如图,已知正方形ABCD,顶点A(1,3)、B(1,1)、C(3,1).规定“把正方形ABCD先沿x轴翻折,再向左平移1个单位”为一次变换.如此这样,连续经过2015次变换后,正方形ABCD的对角线交点M的坐标变为( )| A. | (-2013,2) | B. | (-2013,-2) | C. | (-2014,-2) | D. | (-2014,2) |
20.下列各式中能用平方差公式计算的是( )
| A. | (-x+2y)(x-2y) | B. | (1-5m)(5m-1) | C. | (3x-5y)(3x+5y) | D. | (a+b)(-a-b) |
10. 如图,点C是线段AB上一点,点M是AC的中点,点N是BC的中点,如果MC比NC长2cm,AC比BC长( )
如图,点C是线段AB上一点,点M是AC的中点,点N是BC的中点,如果MC比NC长2cm,AC比BC长( )
 如图,点C是线段AB上一点,点M是AC的中点,点N是BC的中点,如果MC比NC长2cm,AC比BC长( )
如图,点C是线段AB上一点,点M是AC的中点,点N是BC的中点,如果MC比NC长2cm,AC比BC长( )| A. | 2cm | B. | 4cm | C. | 1cm | D. | 6cm |
 如图,在平面直角坐标系中,已知矩形ABCD的三个顶点B(4,0)C(8,0)D(8,8)抛物线y=ax2+bx过A,C两点,动点P从点A出发,沿线段AB向终点B运动,同时点Q从点C出发,沿线段CD向终点D运动,速度均为每秒1个单位长度,运动时间为t秒,过点P作PE⊥AB交AC于点E
如图,在平面直角坐标系中,已知矩形ABCD的三个顶点B(4,0)C(8,0)D(8,8)抛物线y=ax2+bx过A,C两点,动点P从点A出发,沿线段AB向终点B运动,同时点Q从点C出发,沿线段CD向终点D运动,速度均为每秒1个单位长度,运动时间为t秒,过点P作PE⊥AB交AC于点E