题目内容
1.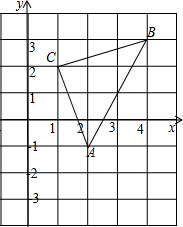 如图,直角坐标系中,△ABC的顶点都在网格点上,其中,C点坐标为(1,2).
如图,直角坐标系中,△ABC的顶点都在网格点上,其中,C点坐标为(1,2).(1)写出点A、B的坐标:A(2,-1)、B(4,3);
(2)求△ABC的面积;
(3)将△ABC先向左平移2个单位长度,再向上平移1个单位长度,得到△A′B′C′,画出△A′B′C′,写出A′、B′、C′三个点坐标.
分析 (1)根据直角坐标系的特点写出对应点的坐标;
(2)用△ABC所在的矩形面积减去三个小三角形的面积即可求解;
(3)分别将点A、B、C先向左平移2个单位长度,再向上平移1个单位长度,得到点A′、B′、C′,然后顺次连接并写出坐标.
解答  解:(1)A(2,-1),B(4,3);
解:(1)A(2,-1),B(4,3);
(2)S△ABC=3×4-$\frac{1}{2}$×2×4-$\frac{1}{2}$×1×3-$\frac{1}{2}$×3×1=5,
故△ABC的面积为5;
(3)所作图形如图所示:
A′(0,0)、B′(2,4)、C′(-1,3).
故答案为:2,-1,4,3.
点评 本题考查了根据平移变换作图,解答本题的关键是根据网格结构作出对应点的位置,然后顺次连接.

练习册系列答案
相关题目
13.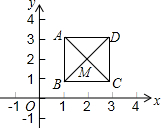 如图,已知正方形ABCD,顶点A(1,3)、B(1,1)、C(3,1).规定“把正方形ABCD先沿x轴翻折,再向左平移1个单位”为一次变换.如此这样,连续经过2015次变换后,正方形ABCD的对角线交点M的坐标变为( )
如图,已知正方形ABCD,顶点A(1,3)、B(1,1)、C(3,1).规定“把正方形ABCD先沿x轴翻折,再向左平移1个单位”为一次变换.如此这样,连续经过2015次变换后,正方形ABCD的对角线交点M的坐标变为( )
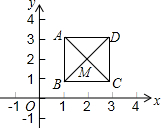 如图,已知正方形ABCD,顶点A(1,3)、B(1,1)、C(3,1).规定“把正方形ABCD先沿x轴翻折,再向左平移1个单位”为一次变换.如此这样,连续经过2015次变换后,正方形ABCD的对角线交点M的坐标变为( )
如图,已知正方形ABCD,顶点A(1,3)、B(1,1)、C(3,1).规定“把正方形ABCD先沿x轴翻折,再向左平移1个单位”为一次变换.如此这样,连续经过2015次变换后,正方形ABCD的对角线交点M的坐标变为( )| A. | (-2013,2) | B. | (-2013,-2) | C. | (-2014,-2) | D. | (-2014,2) |
10. 如图,点C是线段AB上一点,点M是AC的中点,点N是BC的中点,如果MC比NC长2cm,AC比BC长( )
如图,点C是线段AB上一点,点M是AC的中点,点N是BC的中点,如果MC比NC长2cm,AC比BC长( )
 如图,点C是线段AB上一点,点M是AC的中点,点N是BC的中点,如果MC比NC长2cm,AC比BC长( )
如图,点C是线段AB上一点,点M是AC的中点,点N是BC的中点,如果MC比NC长2cm,AC比BC长( )| A. | 2cm | B. | 4cm | C. | 1cm | D. | 6cm |
 利用所示图来证明勾股定理.
利用所示图来证明勾股定理.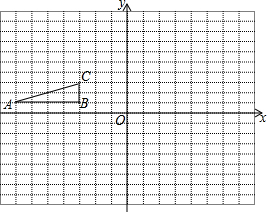 如图,方格纸中的每个小方格都是边长为1个单位的正方形,Rt△ABC的顶点均在格点上,在建立平面直角坐标系后,点A的坐标为(-7,1),点B的坐标为(-3,1),点C的坐标为(-3,3).
如图,方格纸中的每个小方格都是边长为1个单位的正方形,Rt△ABC的顶点均在格点上,在建立平面直角坐标系后,点A的坐标为(-7,1),点B的坐标为(-3,1),点C的坐标为(-3,3). 如图,在平面直角坐标系中,已知矩形ABCD的三个顶点B(4,0)C(8,0)D(8,8)抛物线y=ax2+bx过A,C两点,动点P从点A出发,沿线段AB向终点B运动,同时点Q从点C出发,沿线段CD向终点D运动,速度均为每秒1个单位长度,运动时间为t秒,过点P作PE⊥AB交AC于点E
如图,在平面直角坐标系中,已知矩形ABCD的三个顶点B(4,0)C(8,0)D(8,8)抛物线y=ax2+bx过A,C两点,动点P从点A出发,沿线段AB向终点B运动,同时点Q从点C出发,沿线段CD向终点D运动,速度均为每秒1个单位长度,运动时间为t秒,过点P作PE⊥AB交AC于点E